Polynomial Regression

Polynomial Regression
Description	Polynomial Regression is a supervised learning method in which the relationship between the independent and dependent variables is modeled as an nth degree polynomial.
Why to use	Predictive Modeling
When to use	When the data points are not captured by the Linear Regression Model and the Linear Regression fails in describing the best result clearly.	When not to use	On Textual data.
Prerequisites	If the data contains any missing values, use Missing Value Imputation before proceeding with Polynomial Regression. If the input variable is of categorical type, use Label Encoder. The output variable must be a continuous data type. Linearity – The relationship between the dependent and independent variables should be linear. Independence – The variables should be independent of each other. Normality – The variables should be normally distributed. The Dependent variable (Y) vs. Residuals plot must not follow a pattern. The errors should be normally distributed.
Input	Any continuous data	Output	The predicted value of the dependent variables.
Statistical Methods used	Fit Intercept Dimensionality Reduction	Limitations	It cannot be used on textual data.

Polynomial Regression is located under Machine Learning () under Regression, in the left task pane. Use the drag-and-drop method to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of Polynomial Regression.

Polynomial Regression is a specific case of Linear Regression. In Polynomial Regression, a polynomial equation is fitted between the dependent and independent variables. It establishes a curvilinear relationship between the dependent variable and independent variables. In a curvilinear relationship, the value of the dependent variable changes in a non-uniform manner with respect to the independent variables.

Properties of Polynomial Regression

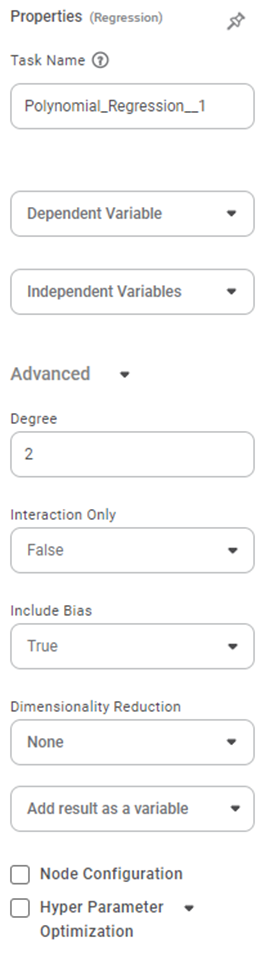
The available properties of Polynomial Regression are as shown in the figure given below.

The table given below describes the different fields present on the Properties pane of Polynomial Regression.

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the name of the task as required.
Dependent Variable		It allows you to select the dependent variable.	You can select only one variable, and it should be of numeric type.
Independent Variables		It allows you to select independent variables.	You can select more than one variable. You can select variables of any type. If categorical or textual variables are selected, you need to use Label Encoders.
Advanced	Degree	It allows you to select the degree of the polynomial equation to be used.	The default value is 2.
	Interaction Only	It allows you to select whether interaction features are to be produced.	The available options are – True and False. If set to True, only interaction features are produced.
	Include Bias	It allows you to select whether bias is to be included.	The available options are – True and False. If set to True, then a bias column, in which all polynomial powers are zero, is included in the output.
	Dimensionality Reduction	It allows you to select the method for dimensionality reduction.	The available options are – None and PCA. The default value is None.
	Add result as a variable	It allows you to select whether the result of the algorithm is to be added as a variable.	For more details, refer to Adding Result as a Variable.
	Node Configuration	It allows you to select the instance of the AWS server to provide control on the execution of a task in a workbook or workflow.	For more details, refer to Worker Node Configuration.
	Hyper Parameter Optimization	It allows you to select parameters for optimization.	For more details, refer to Hyperparameter Optimization.

Example of Polynomial Regression

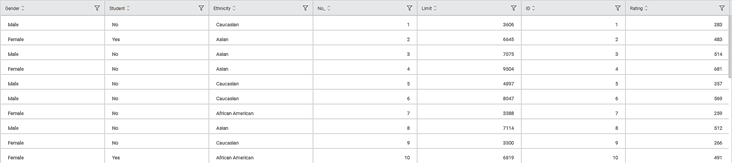
Consider a dataset of Credit Card balances of people of different gender, age, education, and so on. A snippet of input data is shown in the figure given below.

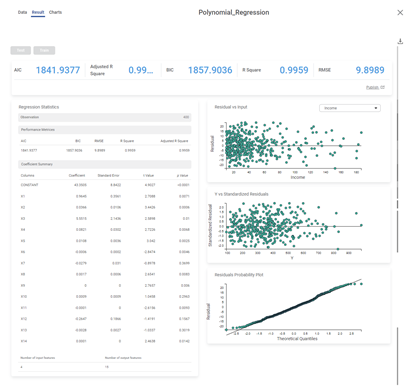
We select Limit, Balance, Income, and Cards as the independent variables and Rating as the dependent variable. The result of the Polynomial Regression is displayed in the figure below.

As seen in the above figure, on the Result page, under the Regression Statistics, the Performance Metrices and Coefficient Summary are displayed.

The table below describes the various performance metrics on the result page.

Performance Metric	Description	Remark
RMSE (Root Mean Squared Error)	It is the square root of the averaged squared difference between the actual values and the predicted values.	It is the most commonly used metric to evaluate the accuracy of the model.
R Square	It is the statistical measure that determines the proportion of variance in the dependent variable that is explained by the independent variables.	Value is always between 0 and 1.
Adjusted R Square	It is an improvement of R Square. It adjusts for the increasing predictors and only shows improvement if there is a real improvement.	Adjusted R Square is always lower than R Square.
AIC (Akaike Information Criterion)	AIC is an estimator of errors in predicted values and signifies the quality of the model for a given dataset.	A model with the least AIC is preferred.
BIC (Bayesian Information Criterion)	BIC is a criterion for model selection amongst a finite set of models.	A model with the least BIC is preferred.

On the Result page, when you scroll down Number of Input and Output features are also displayed, as shown in the figure below.

The result page also shows tables that show Variance Inflation Factor and Feature Importance for each of the selected independent (predictor) variables.

Feature importance refers to methods that assign a score to input features based on how useful they are for predicting the dependent variable.

It indicates the relevance of each of the independent variables to the dependent variable.

Table of Contents