Descriptive Statistics
Description	Descriptive statistics involves the calculation of various statistical measures such as the measure of central tendency, the measure of variability, percentiles, and also the diagrammatic & graphical representation of data.
Why to use	To prove simple summaries about the sample data and its measures.
When to use	When you want to get different statistical values. When you want to find out if there are any missing values in the data.	When not to use	On textual data.
Prerequisites	It should be used on numerical data.
Input	Any dataset that contains numerical data.	Output	Statistical information of the selected features is displayed.
Statistical Methods used	Missing Frequency (only for categorical data) Frequency Percentage (only for categorical data) Mean Standard Deviation Variance Min Q1 Median (Q2) Q3 Max Range Mode Skewness Kurtosis Standard error	Limitations	-

Descriptive Statistics is located under Model Studio ( ) in Data Preparation, in the task pane on the left. Use drag-and-drop method to use algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of Descriptive Statistics.

Descriptive statistics are brief descriptive coefficients that summarize a given data set, which can be either a representation of the entire or a sample of a population. Descriptive statistics are broken down into measures of central tendency and measures of variability (spread).

Measures of Frequency: Count, Percent, and Frequency

Measures of Central Tendency: Mean, Median, and Mode

Measures of Dispersion or Variation: Range, Variance, Standard Deviation

Measure of lack of symmetry: Skewness

Measure of tailedness: Kurtosis

Measure of the statistical accuracy: Standard error

Partition Values: Percentile Ranks, Quartile Ranks.

Properties of Descriptive Statistics

The available properties of Descriptive Statistics are as shown in the figure given below.

The table given below describes different fields present on properties of Descriptive Statistics.

Field		Description	Remark
Task Name		It displays the name of the selected task.	You can click the text field to edit or modify the name of the task as required.
Features		It allows you to select the features for which you want to get statistical information.	Multiple features can be selected. Statistical information is provided only for numerical datatype. Frequency and Frequency Percentage is provided only for categorical datatype.
Advanced	Node Configuration	It allows you to select the instance of the AWS server to provide control on the execution of a task in a workbook or workflow.	For more details, refer to Worker Node Configuration.

Interpretation from Descriptive Statistics

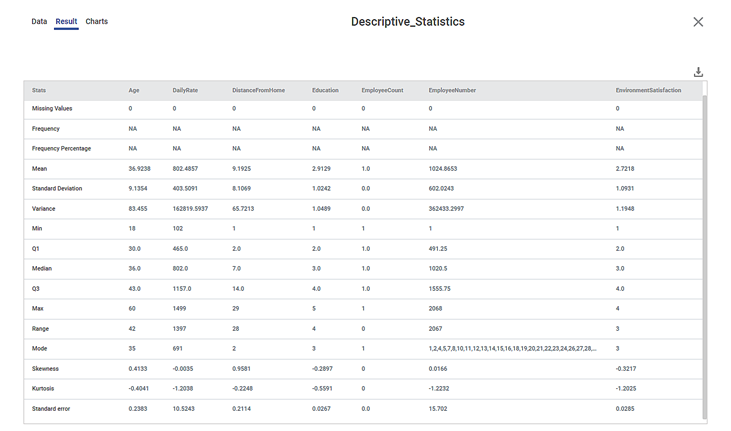
The figure given below displays the output of descriptive statistics used on sample data.

The table given below describes the result for Descriptive Statistics.

Descriptive Statistic	Result	Remark
Total No. of Observations	It provides the total number of observations present in the dataset	It is the total count of the number of rows.
Missing	It shows the number of missing values present in the selected features.	You cannot build some models if data contains missing values. Perform Missing Value Imputation to treat (remove or replace) missing values. Refer to Missing Value Imputation.
Frequency	It provides the frequency of the number of times the data has occurred.	It is calculated only for categorical datatype.
Frequency Percentage	It provides the frequency percentage of the number of times the data has occurred.	It is calculated only for categorical datatype.
Mean	It provides average of the selected features.	It is calculated only for numerical datatype.
Standard Deviation	It measures the dispersion of a dataset relative to its mean.	It is calculated only for numerical datatype. If standard deviation is high, the data is more spread out, and data points are more spread out in the distribution. It is measured as the square root of variance.
Variance	It measures how far a set of numbers are spread out from their average value.	It is calculated only for numerical datatype. It is measured as the average square deviation of each number in the data set from its mean.
Min	It provides the minimum value for the selected features.	It is calculated only for numerical datatype.
Q1	It provides the 25^th percentile of the data.	It is calculated only for numerical datatype. It is the value below which 25% of the observations in the data are found.
Median (Q2)	It provides the middle value for the selected features.	It is calculated only for numerical datatype. It is the value below which 50% of the observations in the data are found.
Q3	It provides the 75^th percentile of the data.	It is calculated only for numerical datatype. It is the value below which 75% of the observations in the data are found.
Max	It provides the maximum value for the selected features.	It is calculated only for numerical datatype.
Range	It is the difference between maximum and minimum value.	It is calculated only for numerical datatype.
Mode	It provides the value that has occurred maximum times.	It is calculated only for numerical datatype. There can be one mode, two modes, or multiple modes present.
Skewness	It provides the distribution of data points. If the value of skewness is less than −1 or greater than +1, the distribution is highly skewed between -1 and 0.5, the distribution is negatively skewed between 0.5 and 1, the distribution is positively skewed between −1 and −0.5 or between +0.5 and +1, the distribution is moderately skewed between −0.5 and +0.5, the distribution is approximately symmetric	It is calculated only for numerical datatype. The skewness value can be positive, zero, negative, or undefined. Right skewed data (positive): right tail is longer, and data is concentrated more towards left. Left skewed data (negative): left tail is longer, and data is concentrated more towards right. Normal distribution (zero): data is symmetrically distributed on both sides of the mean. In other words, If Mean > Median > Mode distribution is positively skewed If Mean < Median < Mode distribution is negatively skewed If Mean = Median = Mode distribution is symmetric
Kurtosis	It identifies whether the tails of a given distributed data contain extreme values.	It is calculated only for numerical datatype. It measures the outliers present in the distribution.
Standard error	It represents the standard deviation of the mean within a dataset. It provides a measurement for the spread of data.	It is calculated only for numerical datatype. The smaller the spread, the more accurate the dataset.

Table of Contents