MLP Neural Network in Regression

MLP (Multi-Layer Perceptron) Neural Network in Regression
Description	An MLP neural network for regression is designed to predict continuous numerical values. It consists of multiple layers, including an input layer, one or more hidden layers, and an output layer. Each layer contains neurons that process the input data and apply activation functions. The network's weights and biases are adjusted during training to minimize the difference between predicted and actual values.
Why to use	1. Non-Linear Mapping 2. Flexibility 3. Universal Approximation 4. Feature Learning 5. Generalization
When to use	1. Non-linear Relationships 2. Complex Data Patterns 3. High-Dimensional Data 4. Unstructured Data 5. Feature Learning 6. Availability of Sufficient Data	When not to use	Linear Relationships Low-Dimensional Data Time and Resource Constraints Interpretable models Noisy Data
Prerequisites	1. Feature Selection or Extraction 2. Labelled Training Data 3. Data Split 4. Data Pre-processing 5. Architecture Design 6. Hyperparameter Tuning 7. Training and optimization 8. Regularization and Early Stopping 9. Evaluation and Testing
Input	Choose a continuous dependent variable (column) and select a specific number (n) of independent variables (columns) with either categorical or numerical types.	Output	1. AIC 2. BIC 3. Adjusted R Square 4. R Square 5. RMSE
Statistical Methods Used	1. Mean Squared Error (MSE) 2. Mean Absolute Error (MAE) 3. R-Squared 4. Cross-Validation 5. Feature Importance 6. Model Selection 7. Hypothesis	Limitations	1. Overfitting 2. Computational Complexity 3. Selection of Hyperparameters 4. Interpretability 5. Data Requirements 6. Lack of Uncertainty Estimation

The MLP Neural Network is located under Machine Learning in Regression, on the left task pane. Alternatively, use the search bar for finding the MLP Neural Network algorithm. Use the drag-and-drop method or double-click to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

An MLP (Multi-Layer Perceptron) neural network in regression refers to a specific type of neural network architecture used for regression tasks. The MLP is designed to predict continuous numerical values as the output.
The MLP consists of multiple layers, including an input layer, one or more hidden layers, and an output layer. Each layer contains a set of interconnected neurons, also known as perceptrons or nodes.

The MLP learns to map the input features to the desired continuous output by adjusting the weights and biases associated with the connections between neurons. These adjustments are made iteratively using optimization algorithms, such as backpropagation, to minimize the difference between the predicted output and the actual target values.

Each neuron in the hidden layers and the output layer applies an activation function to the weighted sum of its inputs. The activation function introduces non-linearities into the model, allowing it to capture complex relationships and patterns in the data.
The MLP can be used to make predictions on new, unseen data. The input features are fed into the network and propagated through the layers. The output value is obtained from the output neuron of the MLP.

Properties of MLP Neural Network in Regression

The available properties of MLP Neural Network are as shown in the figure given below:

Field		Description	Remark
Task Name		It displays the name of the selected task.	You can click the text field to modify the task name as required.
Dependant Variable		It allows you to select the dependent variable.	You can select only one variable, and it should be of Numeric type.
Independent Variable		It allows you to select the independent variable	You can choose more than one variable. You can select between Categorical and Numerical variables. Not any type only categorical and numerical. Because users consider all types try to run with text, geographical, and time series variables
Advanced	Learning_rate	It allows you to select the constant, in-scaling, or adaptive learning rate.	It is a hyperparameter that controls the step size at which the weights and biases of the network are updated during the training process.
	Learning_rate_init	It allows you to enter the learning rate value.	It refers to the initial learning rate used at the beginning of the training process.
	Hidden Layer Sizes	It allows you to enter the number of hidden layers.	It refers to the number of neurons or units in each hidden layer of the network.
	Activation	It allows us to choose no-op, logistic sigmoid, hyperbolic tan, and rectified linear unit functions.	It is a mathematical function applied to the weighted sum of the inputs to each neuron in a hidden layer or the output layer.
	Solver	It allows us to choose lbfgs, sgd, and adam.	It refers to the optimization algorithm used to update the weights and biases of the network during the training process.
	Maximum Iterations	It allows us to enter the number of iterations. The default value is 200.	It refers to the maximum number of iterations or epochs that the training process will run.
	Random State	It allows us to enter the number of random states we want. The default value is 0.	It is a parameter that controls the random initialization of the network's weight and biases.
	Power_t	It allows us to select the power level. The default value is 0.5.	It determines the convergence criterion for the optimization algorithm.
	Dimensionality Reduction	It allows you to select between None and PCA.	It to the process of reducing the number of input features or variables in a dataset while preserving the important information and patterns present in the data.

Example of MLP Neural Network

In the example given below, the MLP Neural Network Regression is applied to the Superstore dataset. The independent variables are Country, City, and Category, etc. Quantity is selected as the dependent variable.

The result page displays the following sections.

Section 1 - Event of Interest

Performance	Description	Remarks
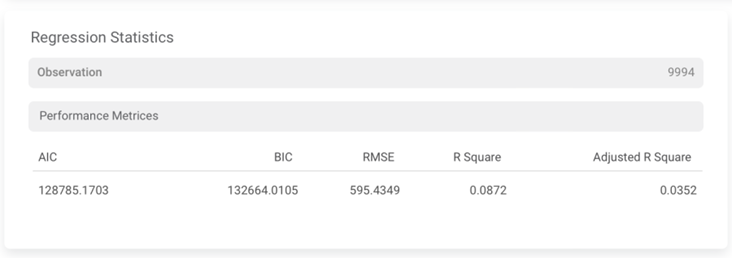
AIC	AIC is an estimator of errors in predicted values and signifies the quality of the model for a given dataset.	A model with the least AIC is preferred.
Adjusted R-Square	It is an improvement of R Square. It adjusts for the increasing predictors and only shows improvement if there is a real improvement.	Adjusted R Square is always lower than R SquareAdd another point as adjusted r Square also considered maximum value which shows the model is the perfect fit for this data. Same for R square. A model with the maximum adjusted R-Square is preferred.
BIC	BIC is a criterion for model selection amongst a finite set of models.	A model with the least BIC is preferred.
R-Square	It is the statistical measure that determines the proportion of variance in the dependent variable that is explained by the independent variables.	Value is always between 0 and 1. The model with maximum R-squared is preferred.
RMSE	It is the square root of the averaged squared difference between the actual values and the predicted values.	It is the most commonly used metric to evaluate the accuracy of the model.

Section 2 – Regression Statistics

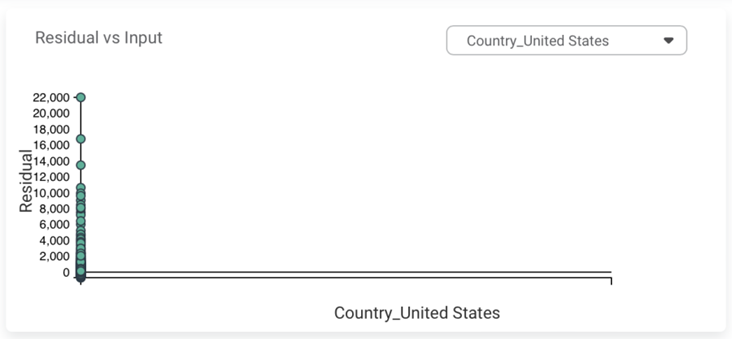
Section 3 – Residuals Vs. Inputs

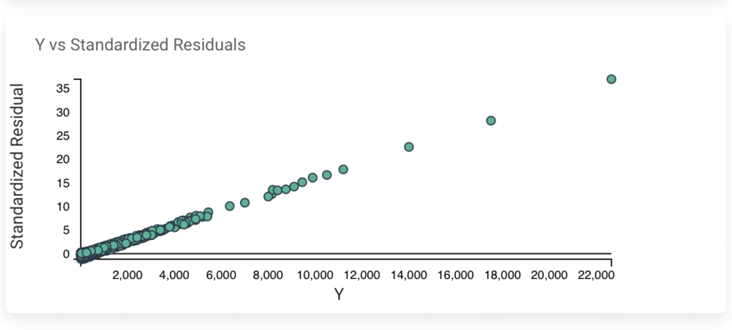
Section 4 – Y Vs. Standardized Residuals

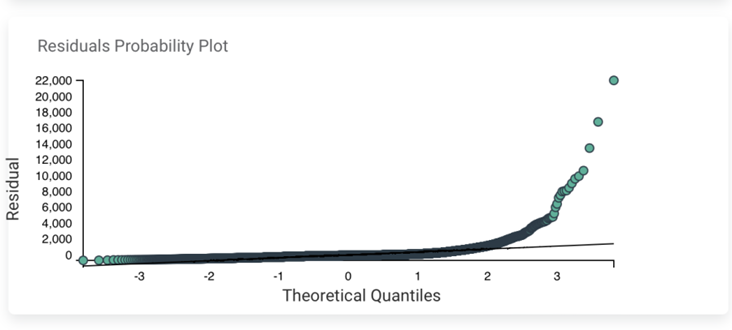
Section 5 – Residuals Probability Plot

Your Rating:

Table of Content