Lasso Regression

Lasso Regression
Description	Lasso Regression is used to penalize the regression method to select a subset of variables by imposing a constraint on model parameters.
Why to use	Predictive Modeling
When to use	For variables having high multicollinearity	When not to use	On textual data.
Prerequisites	If the data contains any missing values, use Missing Value Imputation before proceeding with Lasso Regression. If the input variable is of categorical type, use Label Encoder. The output variable must be a continuous data type. Linearity – The relationship between the dependent and independent variables is linear. Independence – The variables should be independent of each other. Normality – The variables should be normally distributed. The Dependent variable (Y) vs. Residuals plot must not follow a pattern. The errors should be normally distributed.
Input	Any continuous data	Output	The predicted value of the dependent variable
Statistical Methods used	Dimensionality Reduction	Limitations	It cannot be used on textual data.

Lasso Regression is located under Machine Learning ( ) in Regression, in the left task pane. Use the drag-and-drop method to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of Lasso Regression.

Lasso is the abbreviation of Least Absolute Shrinkage and Selection Operator. It is a regression analysis method that uses shrinkage to perform both variable selection and regularization. This usage of shrinkage increases the prediction accuracy and interpretability of a statistical model.
Shrinkage refers to the fact that the data values shrink towards a central point, like the mean. Lasso regression performs L1 regularization in which a penalty equal to the absolute value of the magnitude of coefficients is added. In this case, some coefficients become zero and are eliminated from the model. Also, heavy penalties result in coefficients with values close to zero. This produces simpler models that are easy to analyze.
Thus, Lasso regression encourages simple and sparse models, where models have a smaller number of parameters. It is suitable for models that show great collinearity to automate variable selection or parameter elimination in a model selection.

Properties of Lasso Regression

The available properties of Lasso Regression are as shown in the figure given below.

The table given below describes the different fields present on the properties of Lasso Regression.

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the name of the task as required.
Dependent Variable		It allows you to select the dependent variable.	You can select only one variable, and it should be of numeric type.
Independent Variables		It allows you to select Independent variables.	You can select more than one variable. You can select variables of any type. If categorical or textual variables are selected, you need to use Label Encoders.
Advanced	Alpha	It allows you to enter a constant that multiplies the L1 term.	The default value is 1.0.
	Fit Intercept	It allows you to select whether to calculate the value of constant (c) for your model.	You can select either True or False. Selecting True will calculate the value of the constant. The default value is True.
	Normalization of Data	It allows you to select whether the regressors will be normalized or not.	The values are True and False. This field is ignored when Fit Intercept is set to False.
	Precompute	It allows you to select whether to use a precomputed Gram matrix.	The values are True and False.
	Maximum Iterations	It allows you to select the maximum number of iterations.	The default value is 1000.
	Copy X	It allows you to select whether the feature input data is to be copied or overwritten.	The values are True and False. If set to True, the value is copied; else, it is overwritten.
	Tolerance	It allows you to select the tolerance for the optimization.	The default value is 0.0001.
	Warm Start	It allows you to select whether to reuse the solution of the previous call to fit as initialization.	The values are True and False.
	Positive	It allows you to select whether the coefficients should be positive or not.	The values are True and False. If set to True, the coefficients will be positive.
	Selection	It allows you to determine a coefficient selection strategy.	The values are cyclic and random. If set to random, a random coefficient is updated in each iteration. If set to cyclic, the features are looped sequentially in each iteration. The default value is cyclic.
	Random State	It allows you to enter the seed of the random number generator.	This value is used only when Selection is set to random.
	Dimensionality Reduction	It allows you to select the Dimensionality reduction method.	The options are None and PCA.

Interpretation of Lasso Regression

Lasso Regression performs L1 regularization in order to enhance the accuracy of the prediction. It shrinks the coefficients down.

The equation for Lasso Regression is, y = β₀ + β₁x + (α * |slope|)

The greater the value of α (alpha), the more accurate result you will get.

Example of Lasso Regression

Consider a dataset of Credit Card balances of people of different gender, age, education, and so on. A snippet of input data is shown in the figure given below.

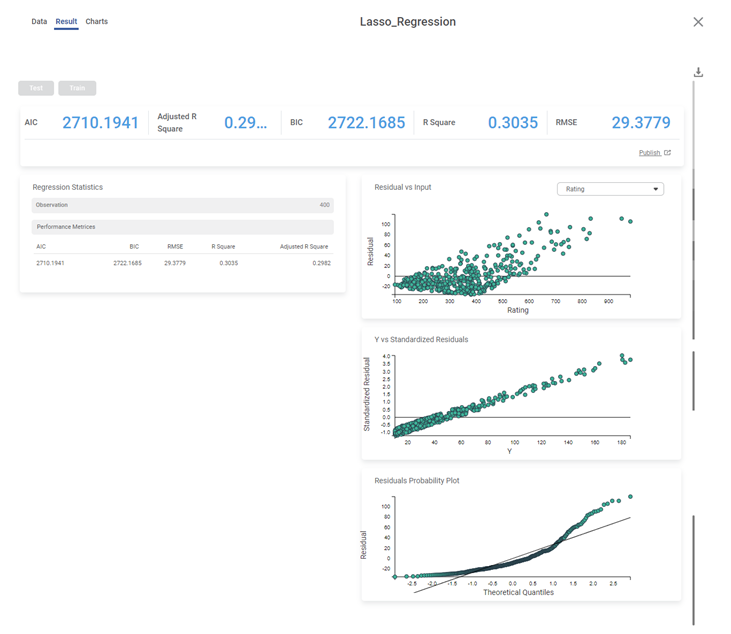
We select Education, Age, and Rating as the independent variables and Income as the dependent variable. The result of the Lasso Regression is displayed in the figure below.

The table below describes the various performance metrics on the result page.

Performance Metric	Description	Remark
RMSE (Root Mean Squared Error)	It is the square root of the averaged squared difference between the actual values and the predicted values.	It is the most commonly used performance metric of the model.
R Square	It is the statistical measure that determines the proportion of variance in the dependent variable that is explained by the independent variables.	Value is always between 0 and 1.
Adjusted R Square	It is an improvement of R Square. It adjusts for the increasing predictors and only shows improvement if there is a real improvement.	Adjusted R Square is always lower than R Square.
AIC (Akaike Information Criterion)	AIC is an estimator of errors in predicted values and signifies the quality of the model for a given dataset.	A model with the least AIC is preferred.
BIC (Bayesian Information Criterion)	BIC is a criterion for model selection amongst a finite set of models.	A model with the least BIC is preferred.

Table of Contents