Random Forest
Description	Random Forest is a Supervised Machine Learning algorithm. It works on the Bagging (Bootstrap Aggregation) principle of the Ensemble technique. Thus, it uses multiple models instead of a single model to make predictions. It is extensively used to solve Classification and Regression problems. In the case of Classification, Random Forest builds multiple decision trees, trains them using the Bagging principle, and generates an output based on a majority vote.
Why to use	To predict a class label based on input data. In other words, to identify data points and separate them into categories.
When to use	When you have a numerical data	When not to use	When you have textual data or data without categorical variables Note: You can add categorical variables by using the label encoding technique.
Prerequisites	The dataset should have at least one categorical variable.
Input	Numerical data containing at least one categorical variable	Output	Labelled or classified data
Statistical Methods used	Accuracy Sensitivity Specificity F-score ROC chart Lift Curve Confusion Matrix	Limitations	It is slow working and difficult to interpret compared to a single decision tree. Its accuracy of prediction is low for complex classification problems.

Random Forest is located under Machine Learning ( ) in Classification, in the left task pane. Use the drag-and-drop method (or double-click on the node) to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of Random Forest.

Properties of Random Forest

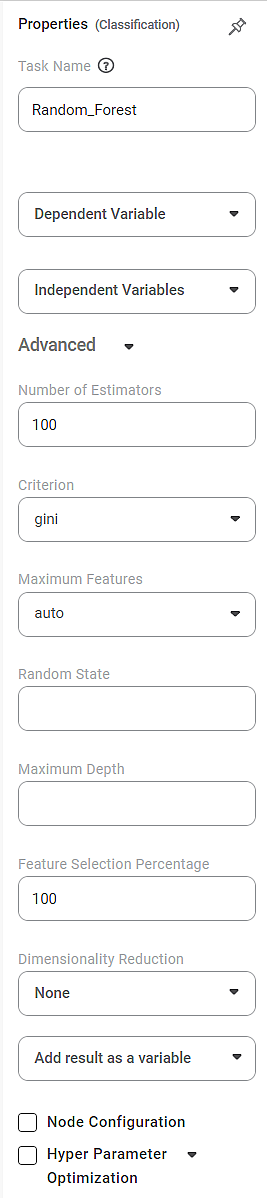
The available properties of the Random Forest are as shown in the figure below.

The table given below describes the different fields present on the properties pane of Random Forest.

Field	Description	Remark
Task Name	It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the task's name.
Dependent Variable	It allows you to select the dependent variable.	Only one feature can be selected. Only categorical values should be selected.
Independent variables	It allows you to select the experimental or predictor variable(s).	Multiple data fields can be selected. Only numerical values should be selected. You can also add categorical columns but first you need to perform label encoding.
Advanced
Number of Estimators	It allows you to select the number of base estimators in the ensemble.	The number of estimators is the number of trees built by the algorithm. The default value is 100. Only numerical values can be entered.
Criterion	It allows you to select the Decision-making criterion to be used.	It is a tree-specific parameter. It decides the quality of the split. The available options are: gini (default) (for Gini impurity) entropy (for Information Gain) For example, you want to select the root node. You can calculate the entropy for each variable, which gives its information gain. The node with maximum information gain is considered the root node. Similarly, the node with a minimum value of the gini index is selected as the root node.
Maximum Features	It allows you to select the maximum number of features to be considered for the best split.	The available options are: auto (default) sqrt log2 none If you select auto, it uses sqrt by default. sqrt, it takes the square root of the number of independent variables as maximum features. log2, it takes the logarithm of the number of independent variables as maximum features. none, it considers all the independent variables as the maximum features.
Random State	It allows you to select a random combination of train and test for the classifier.	It randomizes the data splitting into train and test. It provides different data each time for training and testing the model. The model is expected to return the same result each time, even with different train-test combinations. It ensures that the obtained results can be reproduced. You can enter any integral value as the random state This parameter is optional.
Maximum Depth	It allows you to set the length of the decision tree.	The more the depth of the tree, the more accurate the prediction. However, more depth also takes more time and computation power. So, it is advisable to choose an optimum depth.
Feature Selection Percentage	It is used to decide the feature importance of the selected variable.	It decides the features that would be displayed on the Data tab. Only those features for which the sum of feature importance is less than or equal to the specified value are displayed. The default value is 100, which is equivalent to 1. For a value 1, all features are considered important. You can select any numerical value between 1 and 100. These features are most important for deciding the success of the classification model compared to other features.
Dimensionality Reduction	It allows you to select the dimensionality reduction technique.	The default value is None. Only one data field can be selected. The available options are, None PCA Principal Component Analysis (PCA) maps the data linearly to a lower-dimensional space to maximize the variance of the data in the low-dimensional representation.
Add Result as a Variable	It allows you to select any of the result parameters as the variable.	You can select from the following performance parameters: Accuracy Sensitivity Specificity F-score
Node Configuration	It allows you to select the instance of the AWS server to provide control on the execution of a task in a workbook or workflow.	For more details, refer to Worker Node Configuration.
Hyperparameter Optimization	It allows you to select parameters for Hyperparameter Optimization.	For more details, refer to Hyperparameter Optimization.

Example of Random Forest

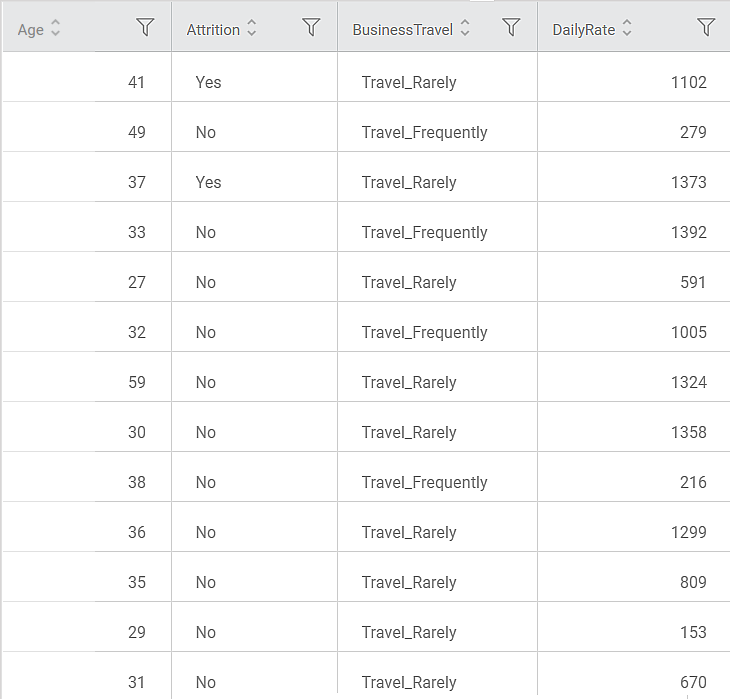
Consider an HR dataset with over 1400 rows and 30 columns. There are multiple features like Attrition, BusinessTravel, DailyRate, PercentSalaryHike, PerformanceRating, and so on in the dataset. The dataset can study the impact of multiple factors on employee attrition.
A snippet of input data is shown in the figure given below.

In the Properties pane, the following values are selected.

Property	Value
Dependent Variable	Attrition
Independent Variables	Age, DailyRate, Education, JobSatisfaction, PercentSalaryHike, StockOptionLevel, WorkLifeBalance
No. of Estimators	100
Criterion	gini
Maximum Features	auto
Random State	3
Maximum Depth	10
Feature Selection Percentage	60
Dimensionality Reduction	None
Add result as a variable	Accuracy, Sensitivity, Specificity, FScore

Notes:

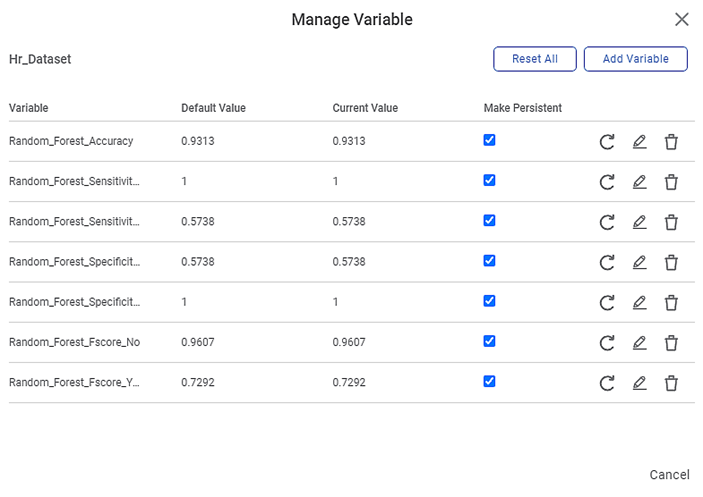
The Feature Selection Percentage selected for configuration is 60, which is equivalent to a value of 0.6. It means that only those features for which the sum of feature importance is less than or equal to 0.6 are displayed in the Data tab.
These features are more important for deciding the success of the classification model compared to other features.

Since we select Accuracy, Sensitivity, Specificity, and FScore as the performance metrics, the following variables are created corresponding to the two Events of Interest, "Yes" and "No.". The value of accuracy remains same for both the events. Thus, you have eight 7 new variables created.
For example, Random_Forest_Accuracy_No, and Random_Forest_Accuracy_Yes are the variables created corresponding to the Accuracy metric for the events "Yes" and "No."

Note:

As you can see, the Default and Current values for each variable are the same, and they are also the values for the performance metrics displayed on the Result page.

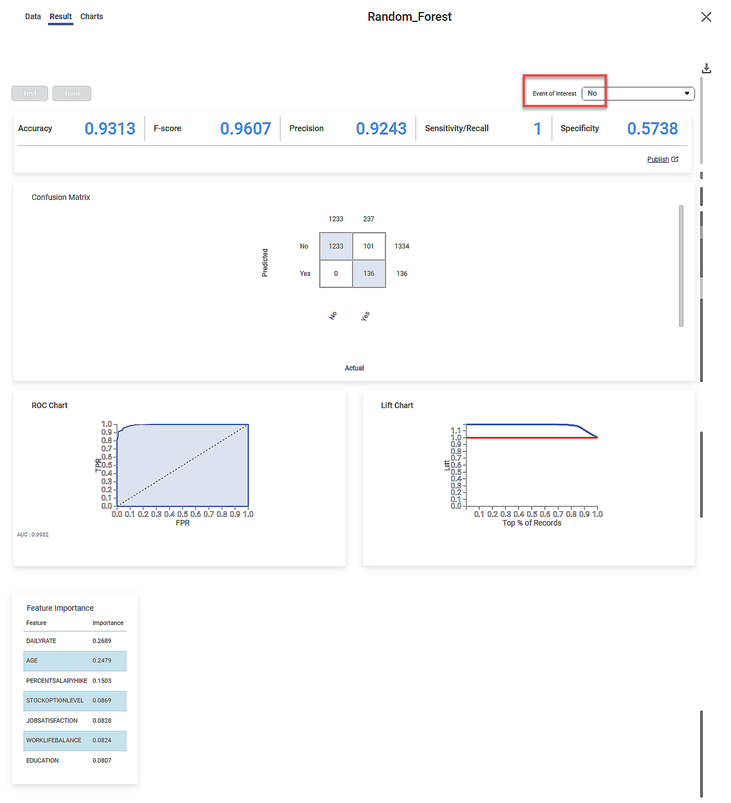
The Result Page for the Event of Interest "No" is shown below.

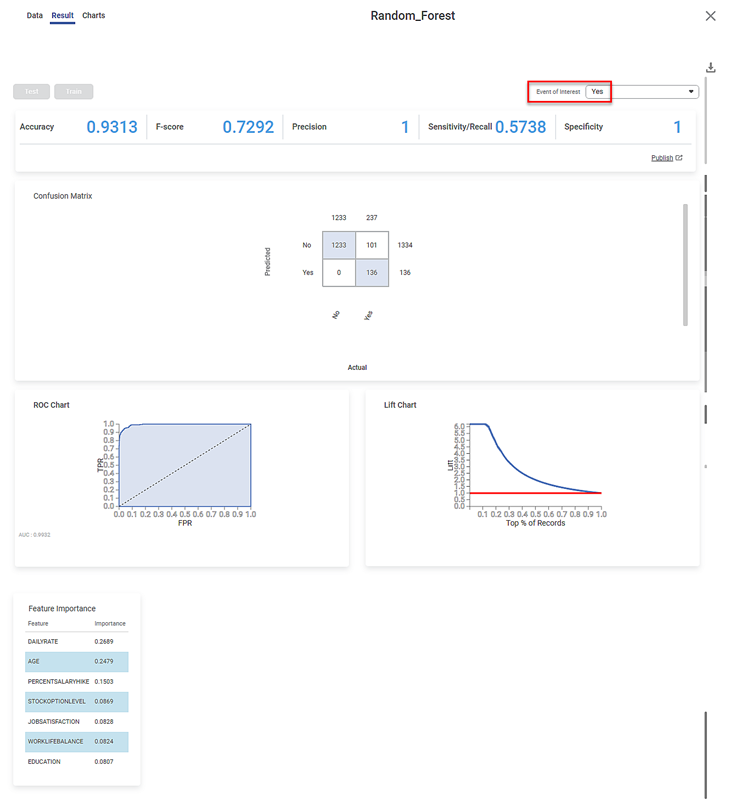
The Result page for the Event of Interest "Yes" is shown below.

The Result page displays

The performance metrics Accuracy, FScore, Sensitivity, and Specificity, for the two events of interest.
You can see that the accuracy for the two events is constant at 0.9313.
The three remaining metrics have different values for the two events.
The Confusion Matrix for the predicted and actual values of the two Events of Interest.
The shaded diagonal cells show the correctly predicted categories. For example, 1233 "No" and 136 "Yes" Attrition values are correctly predicted.
The remaining cells indicate the wrongly predicted categories. For example, 101 "Yes" Attrition values are wrongly predicted as "No."
The Receiver Operating Characteristics (ROC) charts for the two Events of Interest.
You can see that the ROC curve is identical for both events.
The Area Under Curve (AUC) for the ROC chart is 0.9906.
Since the value is high (close to 1), the Random Forest model is meaningful and clearly distinguishes between the two classes or events of interest (of Attrition).
The Lift Charts for the two Events of Interest.
You can see that the Lift Charts are different for the two events
The area of the region between the life curve (blue) and baseline (red) is different for the two events.
Since the area for the Event of Interest "Yes" is more, we can conclude that the Random Forest algorithm more clearly classifies this event.
The Feature Importance of the selected independent variables.
The feature importance is expressed as a decimal number
The features are arranged in descending order of their importance.
Thus, DailyRate is most important while WorkLifeBalance is the least important feature for deciding employee attrition.

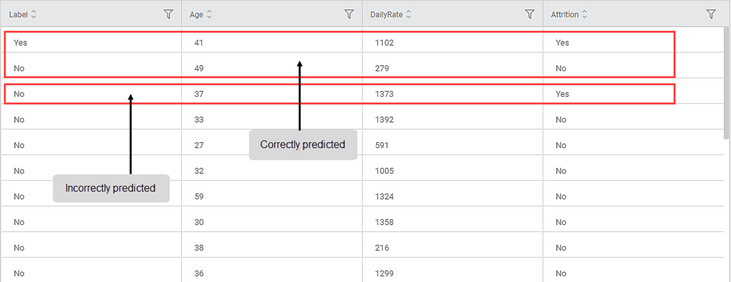
The Data page displays

One additional Label column Two columns: Index and LabelSince the image for the Data tab does not show the index column, should we still add it?No.
The dependent variable column (Attrition)
The maximum importance features, that is, features for which the sum of feature importance is less than or equal to 0.6 (Age and DailyRate)
You can compare the corresponding values in the Label and Attrition columns and observe the correctly and incorrectly predicted values

Table of contents