One-Class SVM Transformation
Description	One-Class Support Vector Machine (One Class SVM) is an unsupervised variation of SVM used for anomaly detection. One-Class SVM is an unsupervised algorithm for outlier detection. It detects whether a new data is similar to or different from the data on which it is trained.
Why to use	To identify whether a data point is an inlier (belonging to the distribution) or an outlier (not belonging to the distribution)
When to use	When the independent variable is numerical when	When not to use	In the case of non-continuous, categorical, or textual variables
Prerequisites	The independent variable should contain any integer or float numerical value. It should not possess any infinite or missing value. You can apply One-Class SVM to a dataset with or without applying the Train-Test Split
Input	Non-clustered data	Output	Clustered data
Statistical Methods Used	Accuracy F-score Sensitivity Specificity Confusion Matrix	Limitations	It is a part of novelty detection (and not outlier detection) It performs better for small samples but underperforms for large samples

One Class SVM is located under Machine Learning ( ) in Anomaly Detection, in the left task pane. Use the drag-and-drop method to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of One-Class SVM.

Properties of One-Class SVM

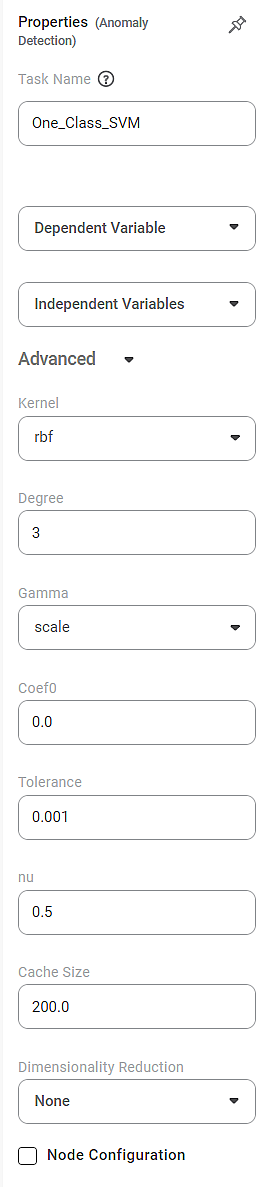
The available properties of One-Class SVM are as shown below.

The table below describes the different fields on the properties of One-Class SVM.

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the task's name. Space between words is not allowed in the Task Name.
Dependent Variable		It allows you to select the dependent variable.	Only one variable can be selected at a time. It is not mandatory to select the dependent variable. It is used to determine the confusion matrix and calculate the following KPIs Accuracy F-score Sensitivity Specificity Error
Independent Variable		It allows you to select Independent variables.	These are the variables used for anomaly detection, that is, to determine the outliers. The independent variable column should not contain any infinite or missing value. You can select more than one variable. The variable should be of continuous numerical type.
Advanced	Kernel	It allows you to select the kernel function to convert your data into a required form.	You can select any one of the following kernel functions: linear poly rbf sigmoid precomputed The rbf (Gaussian radial basis function) function is selected by default.
	Degree	It allows you to select the degree of the polynomial kernel function.	It is applicable only when you select poly as the kernel function. It is ignored in the case of all the remaining kernels. You can insert only integer value for Degree. In the case of any other type of value, you get a validation error. Its default value is 3.
	Gamma	It allows you to select the gamma parameter.	Gamma is the kernel coefficient for the following kernel functions. rbf poly sigmoid Model behavior is extremely sensitive to the gamma parameter. Very small gamma values indicate that the model is constrained (smooth) and cannot capture the data complexity. You can select any one of the following gamma parameters: scale auto By default, the scale parameter is selected. This parameter is not very significant for anomaly detection.
	Coef0	It is used to select the independent term for the kernel function.	The term is significant in the case of the following kernel functions. poly sigmoid The default value is 0.0. This parameter is not very significant for anomaly detection.
	Tolerance	It allows you to set the Tolerance value.	It is the tolerance for the stopping criterion for iterations. It is a parameter used while comparing two values during optimization. The default value is 0.001.
	nu	It allows you to select the value of nu to limit the number of training errors.	Its value lies between zero and one. The default value is 0.5. This parameter is significant for anomaly detection. It is an upper limit for a fraction of training errors and a lower limit for a fraction of support vectors. As the value of nu approaches one (1), the plot gets more scattered.
	Cache Size	It allows you to select the cache size.	It specifies the size of the kernel cache. Cache size is the quantum of memory allotted to the kernel cache maintained in memory. It improves the building time of the model. It is measured in megabytes (MB). The default value is 200.0.
	Dimensionality Reduction	It allows you to select the dimensionality reduction technique.	The default value is None. Only one data field can be selected. The available options are, None PCA Principal Component Analysis (PCA) maps the data linearly to a lower-dimensional space to maximize the variance of the data in the low-dimensional representation.
	Node Configuration	It allows you to select the instance of the AWS server to provide control over the execution of a task in a workbook or workflow.	For more details, refer to Worker Node Configuration.

Example of One-Class SVM

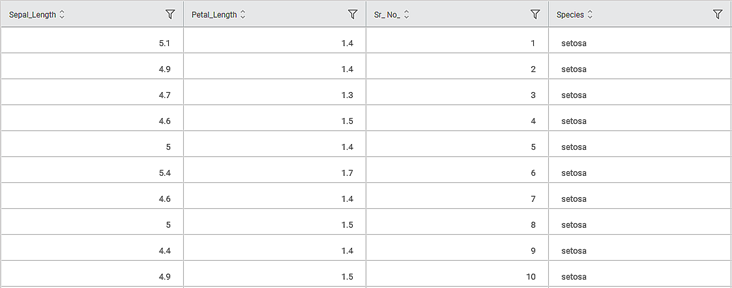
Consider an Iris dataset with two classes of species, Iris-setosa and Iris-versicolor. A snippet of the input data is shown below.

Scenario 1:

We apply One-Class SVM to the input data by selecting the Species column as the Dependent Variable. The selected values are given below.

Property	Value
Dependent Variable	Species
Independent Variable	Sepal Length, Sepal Width, Petal Length, Petal Width
Kernel	rbf
Degree	3
Gamma	scale
Coef0	0.0
Tolerance	0.001
Nu	0.5
Cache Size	200.0

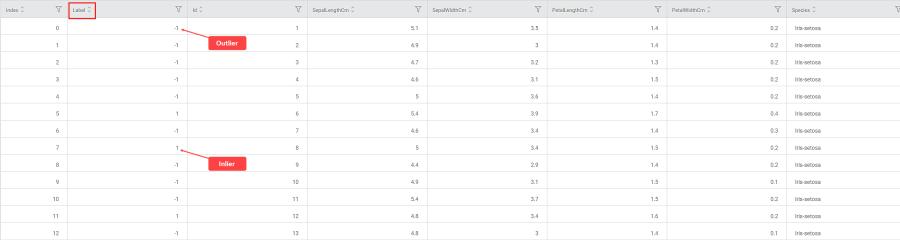
In the Data tab, you see a categorical Label column added to the original data. The Label values decide whether the selected value is Inlier or Outlier.

Label = 1 for an Inlier (represented in Blue in Rubiscape)
Label = -1 for an Outlier (represented in Red in Rubiscape)

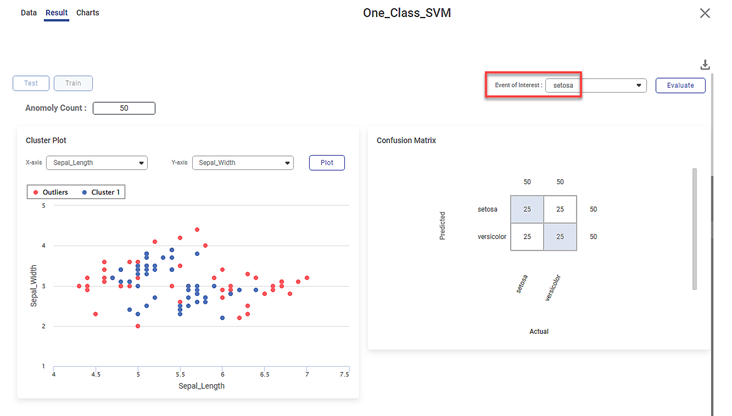
Further, the Result page displays

The following KPIs for the selected event of interest, that is, species
In this case, the event of interest is Iris-setosa
Cluster Plot between two independent variables.
In this case, it is plotted between Sepal Length and Sepal Width
The blue dots represent the inliers, the data points belonging to the distribution. Here, all the blue dots belong to Cluster 1.
The red dots represent the outliers, that is, the data points not belonging to the distribution
You can change the independent variables and observe the cluster plots for different combinations of independent variables
Make sure to select different variables for the cluster plot. If you select the same variable, you see the error message 'Please select different x-axis and y-axis labels.'
Confusion Matrix between the predicted and actual values of the two species.
The shaded diagonal cells show the correctly predicted categories. For example, 14 data points out of 50 for Iris-setosa species are correctly predicted.
The remaining cells indicate the wrongly predicted categories, that is, errors.

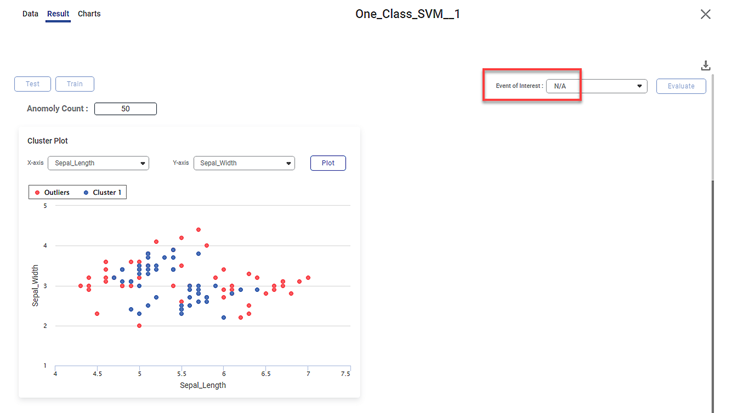
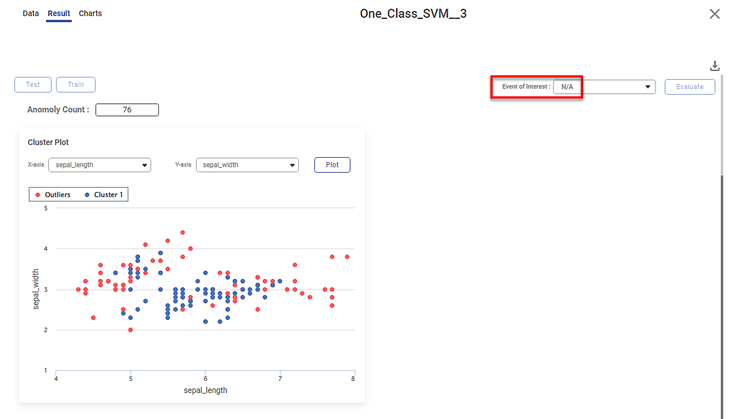
Scenario 2:
We apply One-Class SVM to the input data. However, now we do not select any variable as a dependent variable. The other selected values remain the same.
On the result page, you observe the cluster plot. The KPIs and Confusion Matrix are not displayed since there is no event of interest option.

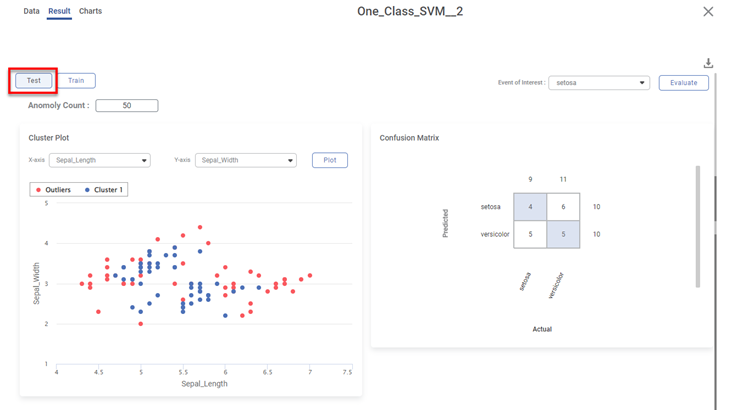
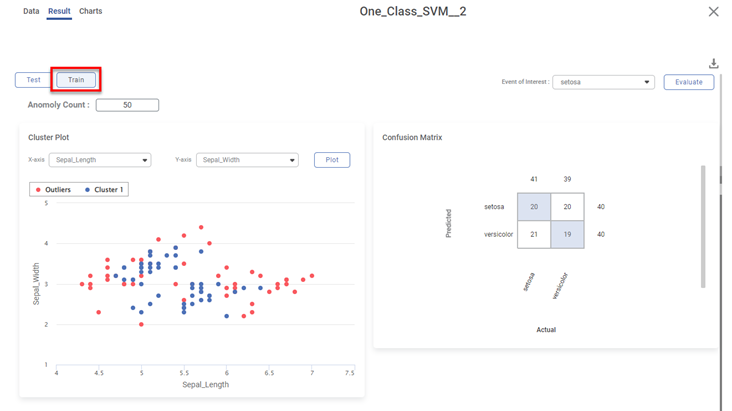
Scenario 3:
We apply the train-test split to the above dataset before applying One-Class SVM.
Various KPIs and Confusion Matrix for Test and Train datasets are different when you explore the results. However, the cluster plot remains the same since it is plotted for the entire dataset.
For example, the figure below displays the result page for the Test dataset.

The figure below displays the result page for the Train dataset.

Scenario 4:
We use a different dataset containing more than two classes. For example, we take an Iris dataset with three classes of species, Iris-setosa, Iris-versicolor, and Iris-virginica.
In this case, run the One-Class SVM algorithm with Species as the dependent variable. When you explore the results, the cluster plot is displayed. However, there is no list of species available in the event of interest field. Hence, KPIs and Confusion Matrix are not displayed.

Table of Contents