Local Outlier Factor
Description	The Local Outlier Factor (LOF) algorithm is an unsupervised machine learning algorithm based on the concept of local density. It compares the density of data points in the distribution to the density of the neighboring data points in the same distribution. The data points that have a significantly lower density than their neighbors are considered outliers.
Why to use	For anomaly detection
When to use	When you want to compare the local density of a data point to the local densities of its neighbors. When you want to identify regions of similar density. When you want to identify data points that have a significantly lower density than their neighbors.	When not to use	On numerical, textual, and interval type data.
Prerequisites	The dependent variable should be of categorical type.
Input	Any dataset that contains categorical data.	Output	Cluster Plot with the outliers highlighted in the plot.
Statistical Methods used	Minkowski distance Cosine distance Euclidean distance Manhattan distance	Limitations	It cannot be used on data other than categorical data.

Local Outlier Factor is located under Machine Learning ( ) in Anomaly Detection, in the task pane on the left. Use the drag-and-drop method (or double-click on the node) to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of Local Outlier Factor.

Local Outlier Factor detects the outliers or deviation of data points in a distribution with respect to the density of its neighbors. It identifies local outliers in a dataset that are not outliers in another region of the dataset.

For example, consider a very dense cluster of data points in a dataset. One of the data points is at a small distance from the dense cluster. This data point is considered an outlier. In the same dataset, a data point in a sparse cluster might appear to be an outlier but is detected to be at a similar distance from each of its neighbors.

A normal data point has a LOF between 1 and 1.5, while an outlier has a much higher LOF. If the LOF of a data point is 10, it means that the average density of its neighbors is ten times higher than the local density of the data point.

The Local Outlier Factor method is used in detecting outliers in geographic data, video streams, or network intrusion detection.

In Rubiscape, the LOF score of a data point is determined using the following:

Number of neighbors
A tree algorithm used for structuring the data
Leaf size to define the depth of the tree algorithm
A metric function to define the distance between two points
Hyperparameter tuning
Dimensionality reduction and variance

Properties of Local Outlier Factor

The available properties of the Local Outlier Factor are as shown in the figure given below.

The table given below describes the different fields present on the Properties pane of the Local Outlier Factor.

Field		Description	Remark
Task Name		It displays the name of the selected task.	You can click the text field to edit or modify the name of the task as required.
Dependent Variable		It allows you to select the variable for which you need to perform the task.	Only one data field can be selected. Only a categorical variable is available.
Independent Variables		It allows you to select the experimental or predictor variable(s).	Multiple data fields can be selected.
Advanced	No. of Neighbors	It allows you to enter the number of neighboring data points.	Only numerical values can be entered. The default value is 20.
	Algorithm	It allows you to select the algorithm used for the search of Nearest Neighbor.	Only one data field can be selected. The available options are, auto Ball Tree KD Tree Brute Force The default value is auto. If auto is selected, the algorithm is selected automatically when the task is executed.
	Leaf Size	It allows you to enter the number of leaf nodes.	Only numerical values can be entered. The default value is 30.
	Metric	It allows you to select the metric function used to define the distance between two points in a dataset.	Only one data field can be selected. The available options are, Minkowski Cosine Euclidean Manhattan The default value is Minkowski.
	Contamination	It determines the proportion of the points with the highest LOF scores (points that are most isolated) to be predicted as anomalies.	It is an automatic hyperparameter tuning method. The default value is auto.
	Dimensionality Reduction	It allows you to select the dimensionality reduction technique. Principal Component Analysis (PCA) maps the data linearly to a lower-dimensional space to maximize the variance of the data in the low-dimensional representation.	Only one data field can be selected. The available options are, None PCA The default value is None.
	Variance	It allows you to enter the variance value.	Only numerical values can be entered. This data field is displayed only if the value of Dimensionality Reduction is selected as PCA.

Example of Local Outlier Factor

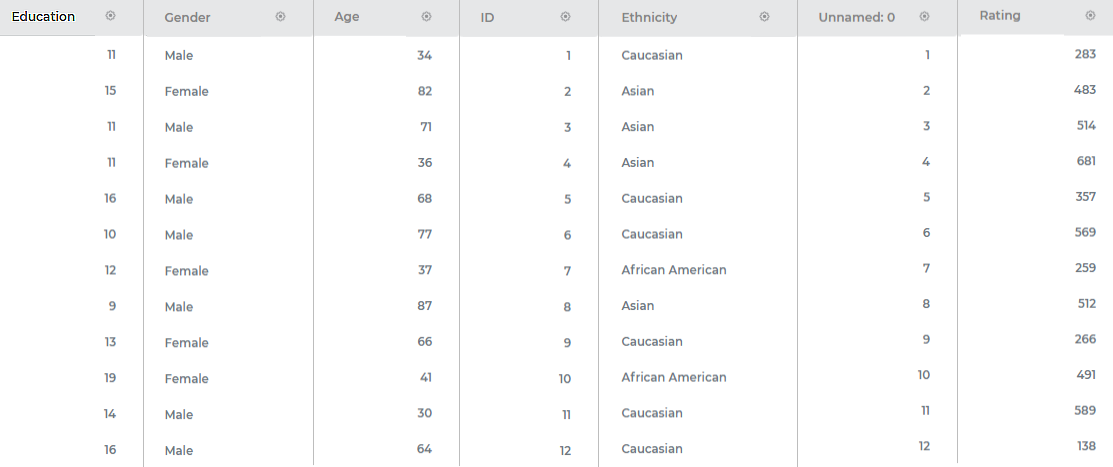
Consider a dataset Credit Card Balance with 13 features and 400 rows. A snippet of the input data is shown in the figure given below.

In the Properties pane of Local Outlier Factor, the values selected are given in the table below.

Property	Value
Dependent Variable	Married
Independent Variables	ID, Income, Limit, Rating, Cards, Age, Education, Balance
No. of Neighbors	20
Algorithm	auto
Leaf Size	30
Metric	Minkowski
Contamination	auto
Dimensionality Reduction	None

The Result page of the Local Outlier Factor is shown in the figure given below.

The Result page initially displays the Cluster Plot based on the default combination of features in the X-axis and Y-axis data fields. To plot a Cluster Plot for different combinations of features, select the respective features from the X-axis and Y-axis drop-downs.

Note:

If you try to plot the Cluster Plot with the same features in the X-axis and Y-axis data fields, then Rubiscape gives an error.

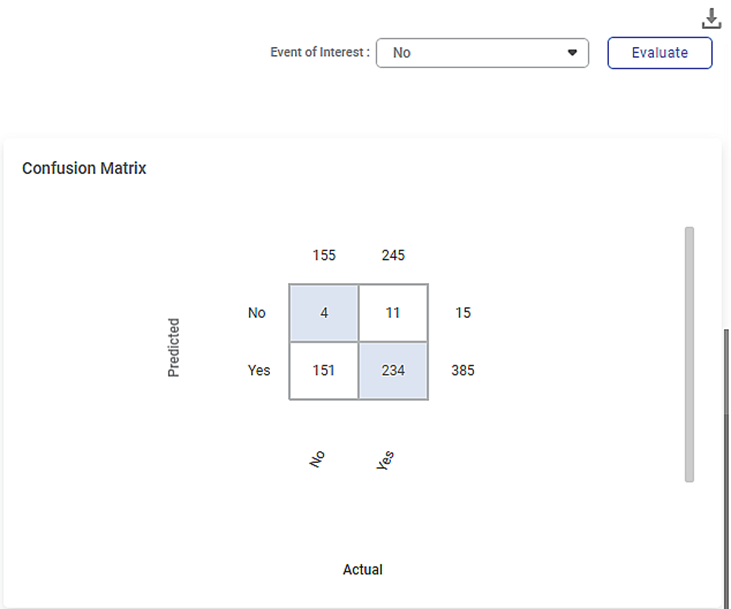
You can also view the Confusion Matrix based on the Event of Interest states of the selected dependent variable. Here, the dependent variable selected is Married, and its Event of Interest states are No and Yes.

To view the Confusion Matrix,

Select either of the values from the Event of Interest drop-down.
Click Evaluate, located in the top-right corner.

The Confusion Matrix is displayed on the right-hand side of the Result page.

The colored boxes in the Confusion Matrix represent the predicted values, while the white boxes represent the error values.

Notes:

Confusion Matrix can be evaluated only if the dependent variable values are displayed in the Event of Interest drop-down.
If Event of Interest displays N/A, the Confusion Matrix cannot be evaluated.
You are required to evaluate a Confusion Matrix based on the selected dependent variable only one time.

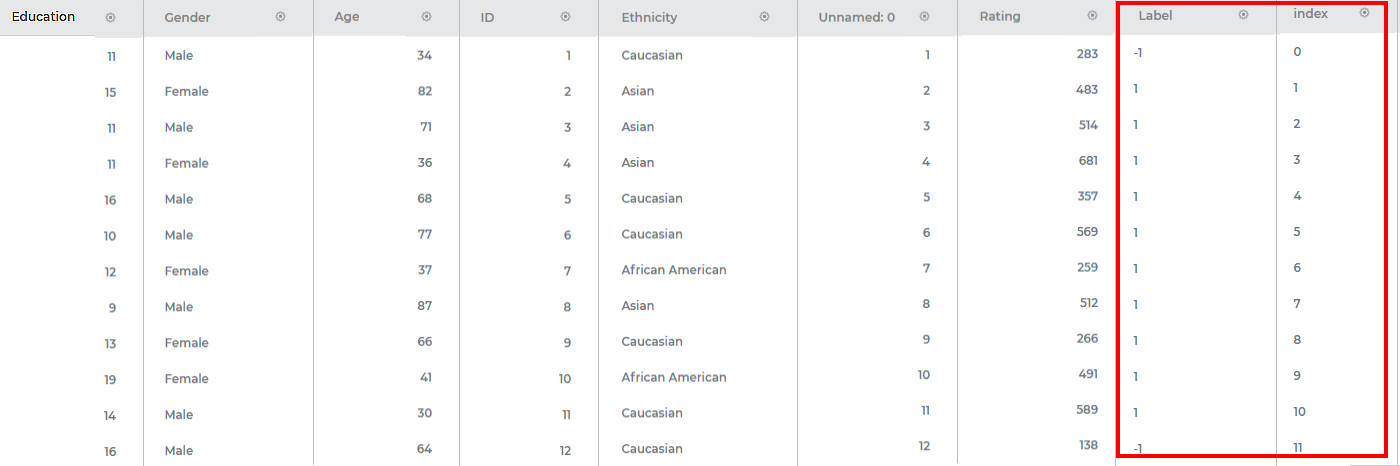
The output Data page displays two more columns, Label and Index, along with the existing 13 features in the LOF result. A snippet of the output data of 15 columns, displayed on the Data page, is shown in the figure below.

Notes:

The rows in the Index column have values starting from 0 until 399.
The Label column has values 1 and -1, where 1 represents cluster data points, and -1 represents the number of outliers.
You can download the data from the Data page using the download icon ( ) located in the top-right.

Interpretation of Result of Local Outlier Factor

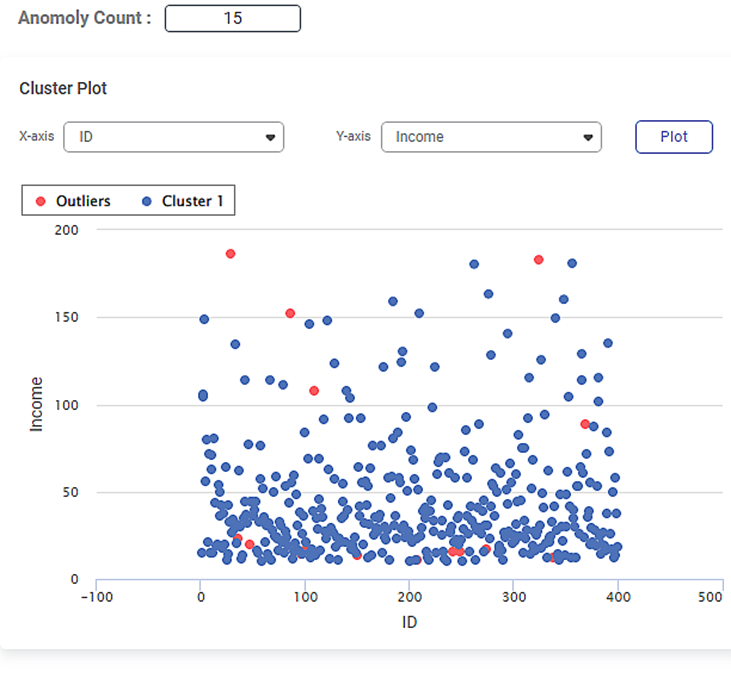
The figure given below shows the Cluster Plot displayed on the LOF Result page.

Some of the key observations from the Cluster Plot are listed below.

The independent variable or label selected in the X-axis data field is
The independent variable or label selected in the Y-axis data field is Income.
The Cluster Plot is plotted between the two labels, one on X-axis (Age) and the other on Y-axis (Income).
The blue dots in the plot represent the cluster of data points in the dataset of 400 data points.
The red dots in the plot represent the local outliers in the cluster of data points.

The figure given below shows the Confusion Matrix displayed on the LOF Result page.

Some of the key observations from the Confusion Matrix evaluated for the selected dataset (of 400 data points) are listed below.

The Confusion Matrix is evaluated for the value No selected from the Event of Interest drop-down.
The blue boxes represent the predicted values.
The white boxes represent the error values.

The table below briefly explains what the values in each of the quadrants of the Confusion Matrix.

Quadrant	Quadrant Value	Description
First (blue)	4	The predicted values of No out of the actual No values (155).
Second (white)	11	The error values of Yes out of the actual Yes values (245).
Third (white)	151	The error values of No out of the actual No values (155).
Fourth (blue)	234	The predicted values of Yes out of the actual Yes values (245).

The value 385 represents the number data points in a cluster density in the dataset of 400 points.
The value 15 represents the number of local outliers in the cluster density in the dataset.

Notes:

The Confusion Matrix is required to be evaluated only once.
The Confusion Matrix evaluated for the value Yes selected from the Event of Interest drop-down remains unchanged.

You can click Publish in the top-right to publish the Local Outlier Factor task as a model. The model can be reused in a workbook for training and experimenting or used in a workflow for production. For more information on publishing a task, refer to Publishing Models.

Table of Contents