Support Vector Machine in Regression

Support Vector Machine In Regression
Description	The Support Vector Machine (SVM) approach for regression is a machine learning technique that seeks to identify a hyperplane that closely resembles the regression function. It reduces deviations (epsilon-insensitive loss) within a predetermined margin. SVM is less prone to overfitting and is capable of handling high-dimensional spaces. However, it may be computationally demanding and necessitate careful kernel and hyperparameter tweaking. For precise prediction tasks, SVM regression is a frequently used method.
Why to use	1. Effective in high-dimensional spaces 2. Robust against outliers 3. Flexibility in kernel selection 4. Control over regularization
When to use	1. Non-linear relationships 2. Limited training data 3. Robustness to outliers 4. High-dimensional feature space 5. Clear margin of separation	When not to use	1. Large datasets 2. Linear relationships 3. High interpretability requirement 4. Noise-dominated datasets 5. Time efficiency
Prerequisites	1. Pre-processing and feature scaling 2. Numerical features 3. Handling outliers 4. Regularization parameter 5. Linear or non-linear relationships 6. Model evaluation 7. Computational resources
Input	Any Continuous Data	Output	1. AIC 2. Adjusted R Square 3. BIC 4. R Square 5. RMSE
Statistical Methods Used	1. Convex Optimization 2. Margin Maximization 3. Loss Function 4. Regularization 5. Kernel Functions 6. Support Vector Selection	Limitations	1. Sensitivity to outliers 2. Difficulty in handling large datasets 3. Determination of appropriate kernel function and parameters 4. Lack of probabilistic outputs 5. Limited effectiveness with high dimensional data

The location of the Support Vector Machine is under Machine Learning in Regression on the feature studio. Alternatively, use the search bar to find Support Vector Machine (SVM) algorithm. Use the drag-and-drop method or double-click to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Support Vector Machine (SVM) in regression is a machine learning algorithm for predicting continuous numerical values. In SVM regression, the goal is to find a hyperplane that approximates the underlying regression function. Support vectors determine the hyperplane; they are the data points closest to the decision boundary.

The equation of the hyperplane is given by: w * x + b = 0

w is a vector perpendicular to the hyperplane and represents the weights of the features.
x is the input vector representing a data point.
b is the bias term.

To make predictions, you can use the sign of the equation w * x + b to determine the class to which a data point belongs. When w * x + b is positive, it means the data point belongs to one class, and when it is negative, it indicates that it belongs to the other class.

The key idea of SVM regression is to minimize the deviations between the predicted and actual values within a specified margin. SVM does not aim to fit all data points precisely. Instead, it seeks a balance between minimizing deviation and maximizing the margin around the hyperplane.
In summary, SVM regression is an algorithm for predicting continuous numerical values. SVM actively finds a hyperplane that approximates the regression function and effectively balances deviations within a margin. Additionally, it utilizes the kernel trick to handle non-linear relationships. Various domains, including finance, economics, and engineering, widely use SVM regression for accurate prediction tasks.

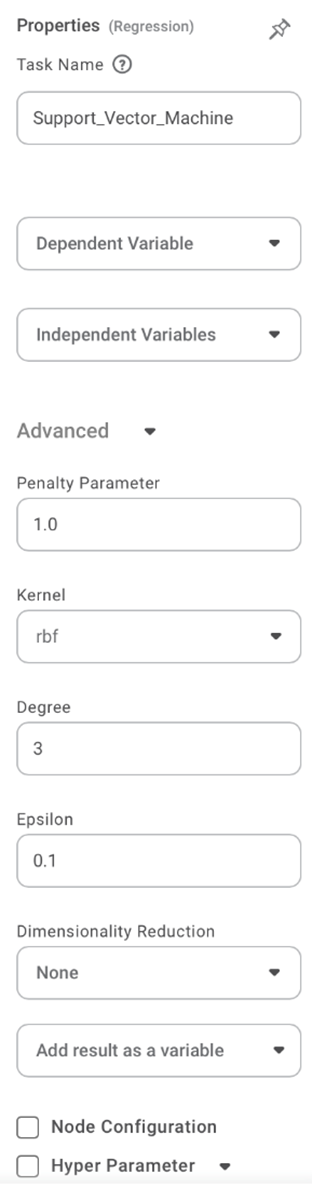
Properties of Support Vector Machine

The figure below shows the available properties of the Support Vector Machine:-

The table given below describes the different fields present on the properties of Lasso Regression.

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the task name as required.
Dependent Variable		You can select the dependent variable from the drop-down list.	You can choose only one data field. Only the numerical data fields selected by the reader are visible.
Independent Variable		It allows you to select the independent variable.	You can choose multiple data fields.
Advanced	Penalty Parameter	It allows you to enter the value of the penalty parameter	Consider this as the degree of correct classification that the algorithm must meet.
	Kernel	It allows you to select through various options of kernels.	Different SVM algorithms use different types of kernel functions.
	Degree	It allows you to select the value of the degree (the default value is 3)	It is the degree of the polynomial function ('poly'), and it ignored by all other kernels
	Epsilon	It allows you to select the value of the epsilon.	It identifies the region of the epsilon tube where there is no penalty in the training loss function for points predicted to be within the epsilon of the actual value.

Example of Support Vector Machine

In the example below, we apply the Support Vector Machine to the Superstore dataset. We select Category, City, Country, etc., as the independent variables, and sales as the dependent variable.
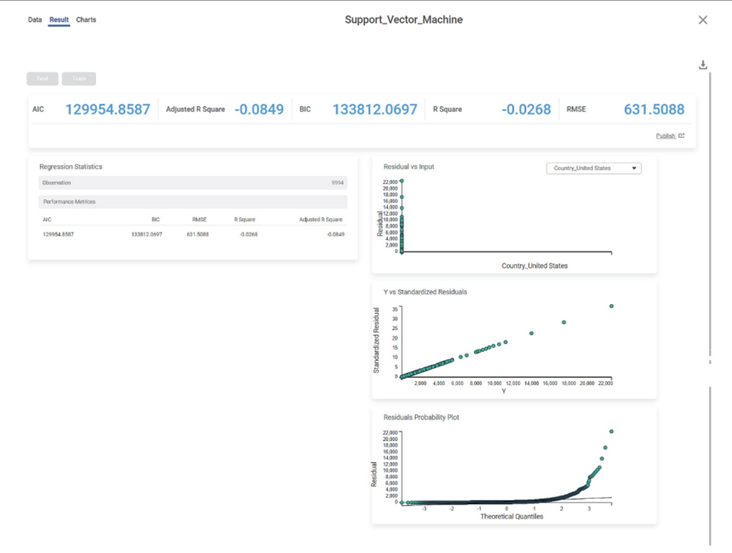
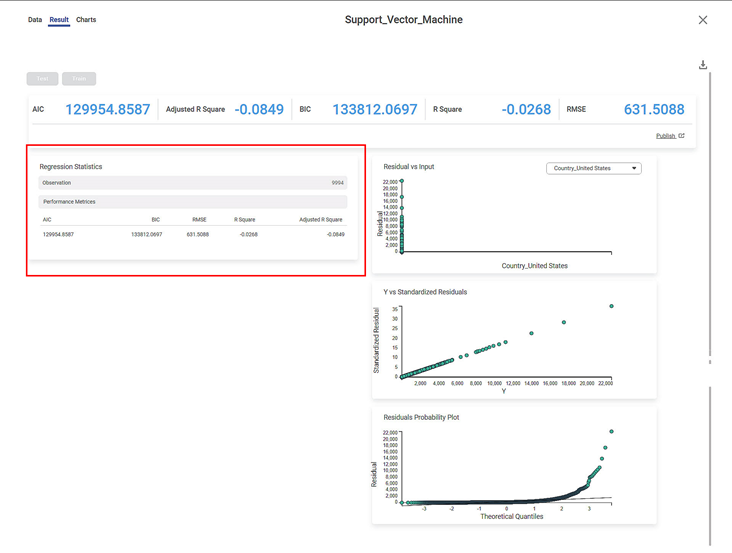
The result page of the Support Vector Machine is displayed below.

The result page displays the following sections.

Key Performance Indicator
Regression Statistics
Graphical Representation

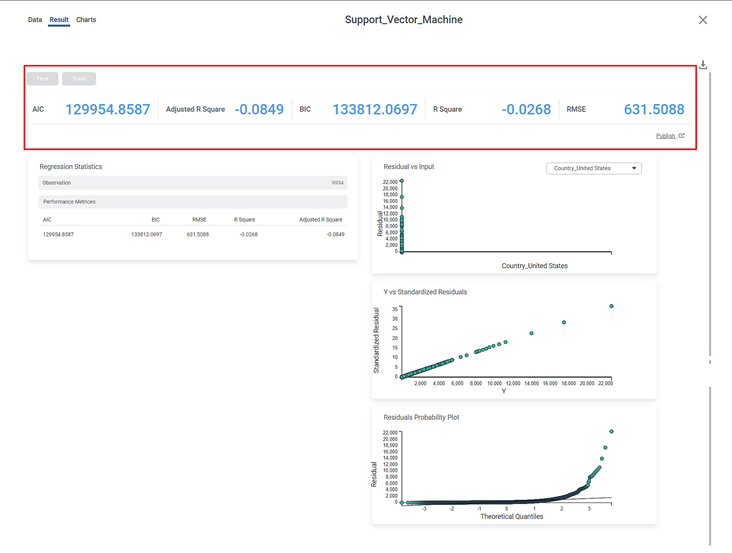
Section 1 - Key Performance Indicator (KPI)

The table below displays various KPIs calculated in Support Vector Machine.

PERFORMANCE	DESCRIPTION	REMARKS
AIC (Akaike Information Criterion)	AIC is an estimator of errors in predicted values and signifies the quality of the model for a given dataset.	A model with the least AIC is preferred.
Adjusted R-Square	It is an improvement of R Square. It adjusts for the increasing predictors and only shows improvement if there is a real improvement.	Adjusted R Square is always lower than R Square.
BIC	BIC is a criterion for model selection amongst a finite set of models.	A model with the least BIC is preferred.
R-Square	The statistical measure determines how much of the variance in the dependent variable is explained by the independent variables.	R-Square is always greater than the Adjusted R-Square.
RMSE	It represents the square root of the average squared difference between the actual values and the predicted values.	It is the most commonly used metric to evaluate the accuracy of the model.

Section 2 – Regression Statistics

The Regression Statistics consist of Observation and Performance metrics.
The Observation displays the total number of rows considered in the Support Vector Machine.
The Performance Matrices consist of all KPI details.

Section 3 – Graphical Representation

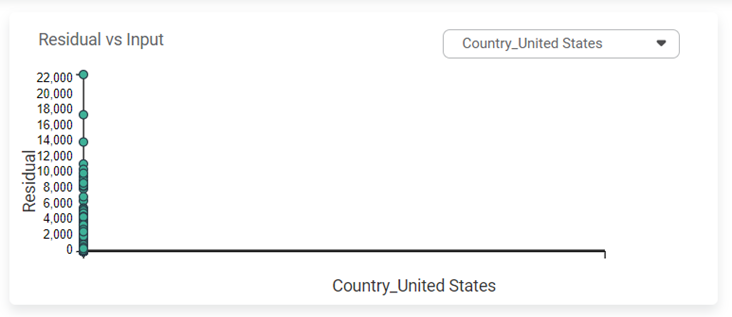
Residuals vs inputs

If this graph creates a pattern, then the sample is improper.
The graph is plotted with the Independent variable on the x-axis and Residual points on the y-axis.
On the right side, there is an independent variable dropdown. In this example, independent variables City, Country, and Category appear in the dropdown.
The input variable is the same as in the dropdown. In the figure below, the input variable is Country, the same as in the dropdown.
If this graph follows a pattern then the data is not normally distributed.

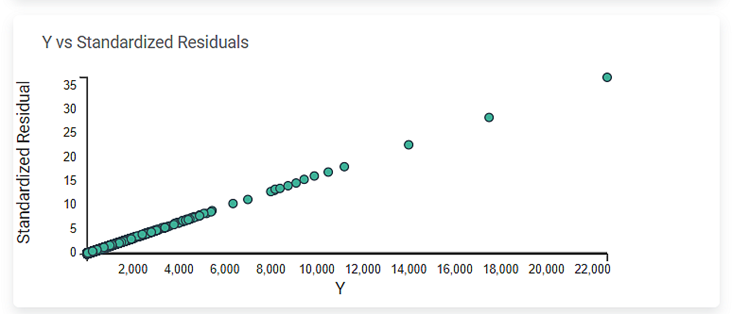
Y vs. Standardized Residuals

The Y vs. Standardized Residuals graph plots the dependent variable, Sales, on the x-axis and the Standardized Residual on the y-axis.

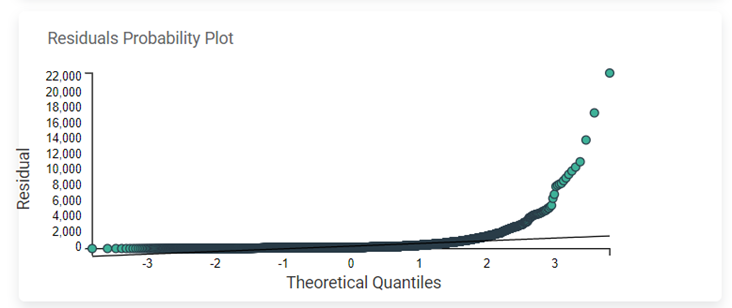
Residuals Probability Plot

The Residuals Probability plot depicts the independent variable on the x-axis and standardized residuals on the y-axis. Its purpose is to identify whether the error terms exhibit a normal distribution.

Your Rating:

Table of Content