Extreme Gradient Boost Regression (XGBoost)

Extreme Gradient Boost Regression (XGBoost)
Description	Extreme Gradient Boost (XGBoost) Regression is a Decision tree-based ensemble algorithm that uses a gradient boosting framework.
Why to use	Predictive Modeling
When to use	When high execution speed and model performance is required.	When not to use	On textual data.
Prerequisites	If the data contains any missing values, use Missing Value Imputation before proceeding with XGBoost Regression. If the input variable is of categorical type, use Label Encoder. The output variable must be a continuous data type.
Input	Any continuous data.	Output	The predicted value of the dependent variable.
Statistical Methods used	Dimensionality Reduction	Limitations	It cannot be used on textual data.

XGBoost Regression is located under Machine Learning ( ) in Regression, in the left task pane. Use the drag-and-drop method to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.
Refer to Properties of XGBoost Regression.

XGBoost is the abbreviation of EXtreme Gradient Boost. It is an ensemble model that combines different machine learning models to get a single prediction. XGBoost turns weak learning models into strong learning models by focusing on the errors in the individual models. In XGBoost, the individual models train upon the residuals (Predicted Result – Actual Result) in each boosting round. XGBoost focuses on speed enhancements using parallel computing and cache mechanism.

Properties of XGBoost Regression

The available properties of XGBoost Regression are as shown in the figure given below.

The table given below describes the different fields present on the Properties pane of XGBoost Regression.

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the name of the task as required.
Dependent Variable		It allows you to select the dependent variable.	You can select only one variable, and it should be of numeric type.
Independent Variables		It allows you to select Independent variables.	You can select more than one variable. You can select variables of any type. If categorical or textual variables are selected, you need to use Label Encoder.
Advanced	Learning Rate	It allows you to enter the boosting learning rate.	The default value is 0.3.
	Number of Estimators	It allows you to enter the Number of gradient boosted trees. It is equivalent to the number of boosting rounds.	The default value is 100.
	Maximum Depth	It allows you to enter the maximum tree depth for base learners.	The default value is 6.
	Booster Methods	It allows you to select the booster to use at each iteration.	The available options are – gbtree, gblinear, and dart. The default selection is gbtree.
	Alpha	It allows you to enter a constant that multiplies the L1 term.	The default value is 0.
	Lambda	It allows you to enter a constant that multiplies the L2 term.	The default value is 1.
	Gamma	It allows you to enter the minimum loss reduction required to make a further partition on a leaf node of the tree.	The default value is 0.
	Sub Sample rate	It allows you to enter the fraction of observations to be randomly sampled for each tree.	The default value is 1.
	Column sample for tree	It allows you to enter the number of columns to be randomly sampled for each tree.	The default value is 1.
	Column sample for level	It allows you to enter the subsample ratio of columns for each level.	The default value is 1.
	Column sample for node	It allows you to enter the subsample ratio of columns for each node.	The default value is 1.
	Random State	It allows you to enter the seed of the random number generator.	—
	Dimensionality Reduction	It allows you to select the dimensionality reduction method.	The options are None and PCA. The default selection is None.
	Add result as a variable	It allows you to select whether the result of the algorithm is to be added as a variable.	For more details, refer to Adding Result as a Variable.
	Node Configuration	It allows you to select the instance of the AWS server to provide control on the execution of a task in a workbook or workflow.	For more details, refer to Worker Node Configuration.
	Hyper Parameter Optimization	It allows you to select parameters for optimization.	For more details, refer to Hyper Parameter Optimization.

Example of XGBoost Regression

Consider a dataset of Credit Card balances of people of different gender, age, education, and so on. A snippet of input data is shown in the figure given below.

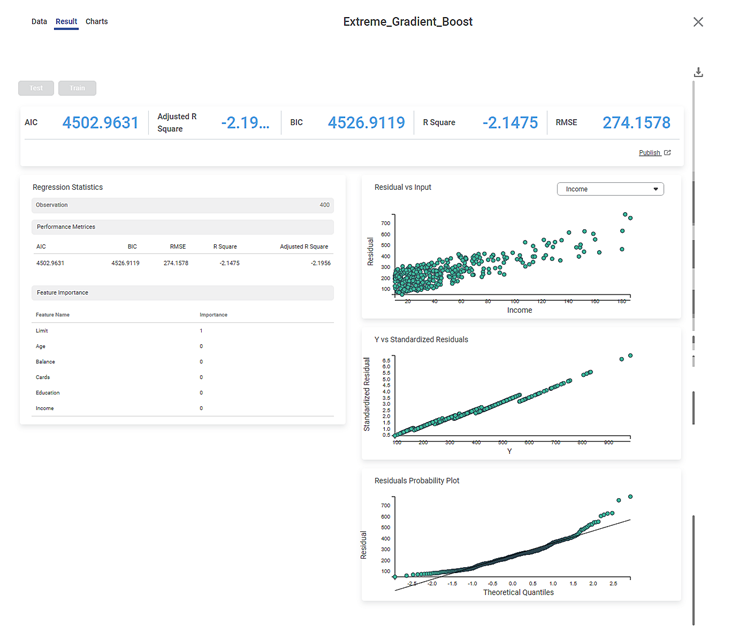
We select Income, Limit, Cards, Education, Age, and Balance as the independent variables and Rating as the dependent variable. The result of the XGBoost Regression is displayed in the figure below.

As seen in the above figure, on the Result page, under the Regression Statistics, the Performance Metrices, Variance Inflation Factor, and Feature Importance of all the features selected as independent variables are displayed.
The table below describes the various performance metrices on the result page.

Performance Metric	Description	Remark
RMSE (Root Mean Squared Error)	It is the square root of the averaged squared difference between the actual values and the predicted values.	It is the most commonly used performance metric of the model.
R Square	It is the statistical measure that determines the proportion of variance in the dependent variable that is explained by the independent variables.	Value is always between 0 and 1.
Adjusted R Square	It is an improvement of R Square. It adjusts for the increasing predictors and only shows improvement if there is a real improvement.	Adjusted R Square is always lower than R Square.
AIC (Akaike Information Criterion)	AIC is an estimator of errors in predicted values and signifies the quality of the model for a given dataset.	A model with the least AIC is preferred.
BIC (Bayesian Information Criterion)	BIC is a criterion for model selection amongst a finite set of models.	A model with the least BIC is preferred.

The result page also shows tables that show Feature Importance for each of the selected independent (predictor) variables.
Feature importance refers to methods that assign a score to input features based on how useful they are for predicting the dependent variable. It indicates the relevance of each of the independent variables to the dependent variable.

Your Rating:

TABLE OF CONTENT