SARIMA
Description	SARIMA is an abbreviation for Seasonal Autoregressive Integrated Moving Average. It is an extension of ARIMA used to model seasonal time series. SARIMA considers the events occurring at regular intervals and impacting the target variable similarly every time. Seasonality is the recurrence of impact-causing events at a fixed frequency.
Why to use	SARIMA is used to model seasonal time series
When to use	To model seasonal time-series data	When not to use	When the data does not contain seasonal factor
Prerequisites	Time-series data should not contain null or missing values.
Input	A time-series data with seasonality	Output	Forecasting Chart Predicted values with Standard Error
Statistical Methods Used	Average Root Mean Square Error	Limitations	--

SARIMA is located under Forecasting( ) in Modeling, in the left task pane. Use the drag-and-drop method to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of SARIMA.

ARIMA supports data with a trend but no seasonality. SARIMA explicitly handles the seasonal component in the univariate data. Thus, SARIMA effectively forecasts time series with univariate data containing trends and seasonality. While applying SARIMA, the hyperparameters of both the trend and seasonal elements are configured. These are,

Trend Elements: p, d, and q
Seasonal Elements: P, D, and Q

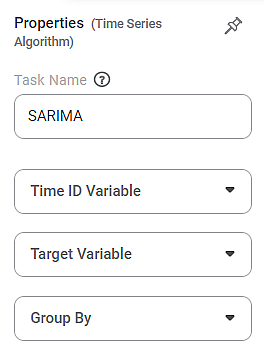
Properties of SARIMA

The available properties of SARIMA are as shown in the figures given below. Figure below shows the basic configurations for SARIMA.

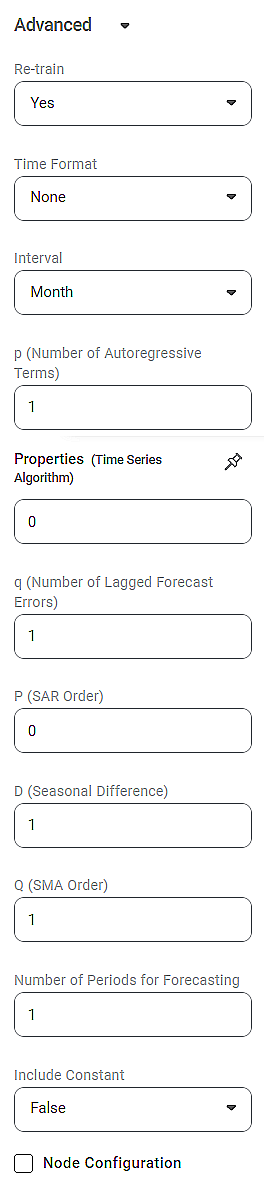
Figure below shows the configuration of advanced properties of SARIMA. They include the trend and seasonal elements, the number of periods to be forecasted, and a regressive constant.

The table given below describes the different fields present on all the properties of SARIMA.

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the task's name as required. Space between words is not allowed in the Task Name.
Time ID Variable		It allows you to select the time variable.	The dataset should contain at least one time variable.
Target Variable		It allows you to select the variable for performing the SARIMA.	The variable selected should be discrete.
Group By		It allows you to select the function for grouping identical data.	Identical values of a column variable in different rows are grouped. Usually, the variable selected is categorical. Selecting Group By is optional
Advanced	Re-train	It allows you to select whether you want to re-train the SARIMA model.	It has two options, Yes and No. By default, the re-train option is Yes.
	Time Format	It allows you to select the time format for the Time ID variable.	–
	Interval	It allows you to select the interval you want to calculate the SARIMA.	The available options are: Day Week Month Quarter Year By default, the interval is set to Month.
	p	It allows you to select the Number of Autoregressive Terms.	By default, p = 1.
	d	It allows you to select the Number of Nonseasonal Differences.	By default, d = 0.
	q Number of Lagged Forecast Errors	It allows you to select the Number of Lagged Forecast Errors.	By default, q = 1.
	P	It allows you to select the SAR Order, the seasonal autoregressive order.	By default, P = 0.
	D	It allows you to select the Seasonal Difference.	By default, D = 1.
	Q	It allows you to select the SMA Order, the seasonal moving average order.	By default, Q = 1.
	Number of Periods for Forecasting	It allows you to select a specific number of periods you want to forecast based on the SARIMA results.	By default, the number of periods selected for forecasting is one (1). You can select any integral number of periods as required.
	Include Constant	It allows you to choose whether you want to include the constant of the regression analysis equation.	It has two options, False and True. False indicates that the constant is NOT included. True indicates that the constant is included. By default, the option selected is False.
	Node Configuration	It allows you to select the instance of the AWS server to provide control on the execution of a task in a workbook or workflow.	For more details, refer to Worker Node Configuration.

Example of SARIMA

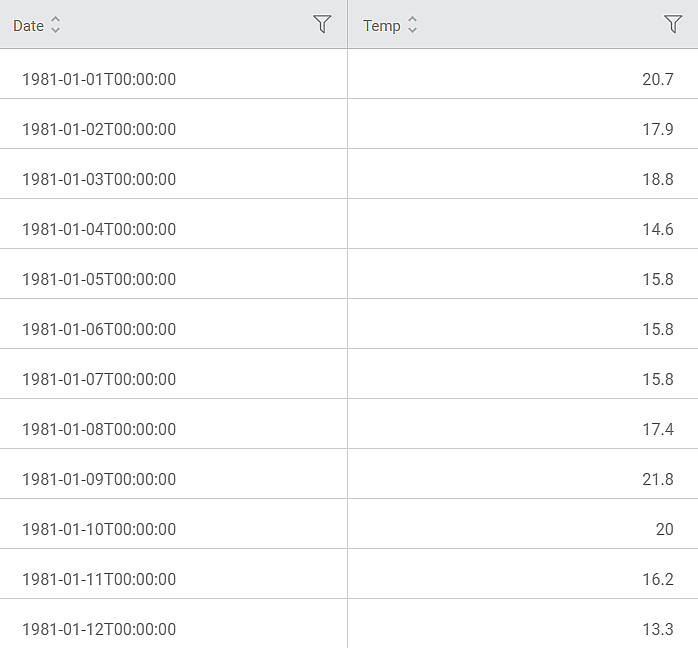
Consider a Temperature dataset with 10 records. It contains columns for Date and corresponding daily temperature. A snippet of the input data is shown in the figure given below.

We apply SARIMA to the input data. The selected values for SARIMA are given below.

Property	Value	Property	Value
Time ID Variable	Date	q	1
Target Variable	Temp	P	0
Group By	—	P	1
Retrain	Yes	D	1
Time Format	12-13-1947	Q	1
Interval	Month	Number of Periods for Forecasting	1
p	1	Include Constant	False
d	0

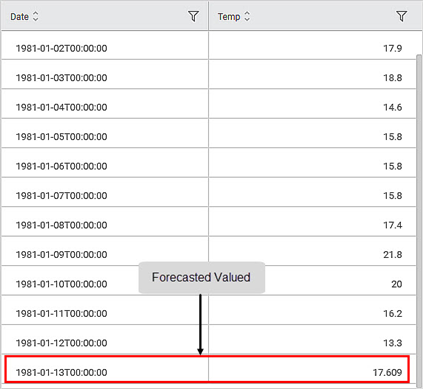
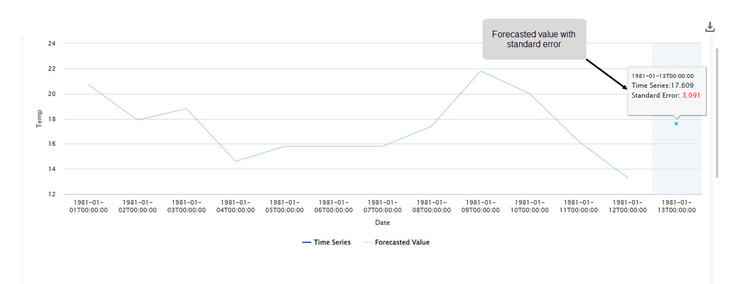
On the Data pane, you see the forecasted value for the last month.

Further, the Result page displays

Forecasting plot of the variation in temperature with Date
Forecasted Value at the end of the plot
Standard Error in the calculation of the forecasted value.

As you can see, the forecasted temperature value for 1981-01-13 is 17.609 with a standard error of 3.091.

Table of Contents