Hyperparameter Optimization in Adaboost

Hyper Parameter Optimization is used for better Optimization of a given dataset. This feature provides you with a list of parameters that give the best solution for your dataset, among the parameters provided for optimizing the solution. You can select more than one parameter from the list.

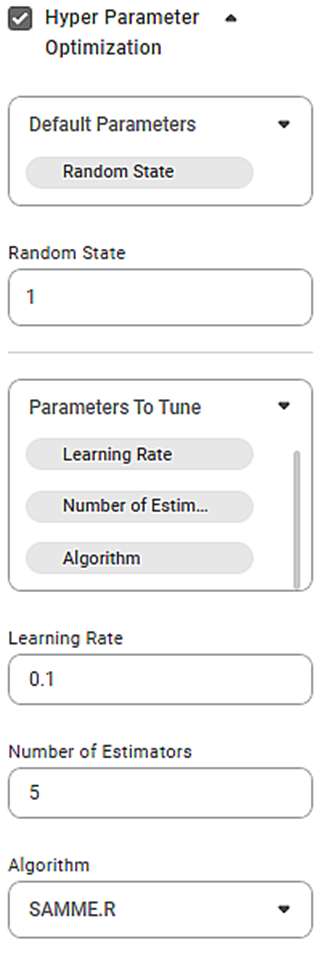
The figure below shows various selections of parameters and other properties for Hyperparameter Optimization in Adaboost.

While selecting various parameters, note that,

• You can select anyone, multiple, but NOT ALL variables as default parameters from the Default Parameter drop-down. If you select all the variables, then you get a validation error for the selection.
• You can choose not to select any variable as the default parameter.
• After you select the default parameter(s), the remaining parameters appear for selection in the Parameter To Tune drop-down.
• You can select all variables in the Parameters To Tune options. In this case, there are NO variables selected as Default Parameters.
• If a variable is selected as default parameter, the same cannot be selected for tuning. If you select it for tuning, the parameter is removed from the default parameter selection.
• You can select any number of values for all the variables. The values should be entered in the appropriate boxes with a comma separating two values.

We select the following values for parameters and properties.

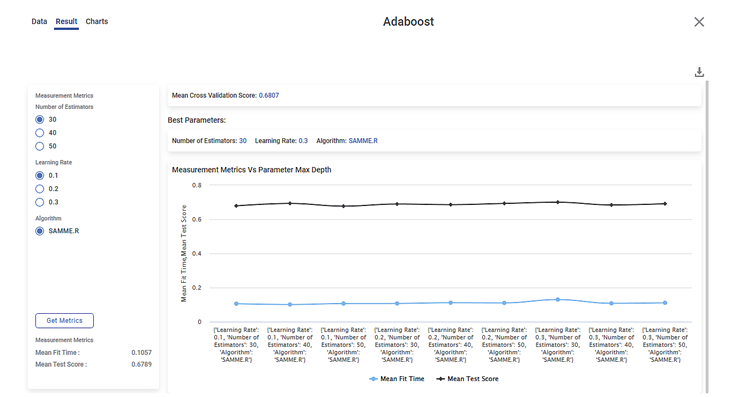
The figure below shows the results of Hyperparameter Optimization in Adaboost.

Inferences:

• The Result page shows
  • Measurement Metrics
  • Best parameters
  • Graphical representation of the variation of Measurement Metrics against Parameter Maximum Depth.
• For example, when Number of Estimators = 30, Learning Rate = 0.1, and Algorithm = SAMME.R,
  • Mean Fit Time = 0.1057
  • Mean Test Score = 0.6789
  • Mean Cross Validation Score = 0.6807
• Best parameters:
  • Number of Estimators = 30
  • Learning Rate = 0.3
  • Algorithm = SAMME.R
• You can change the selected values and get new Measurement Metrics by clicking the Get Metrics button.
• The graph contains two curves for
  • Mean Fit Time
  • Mean Test Score
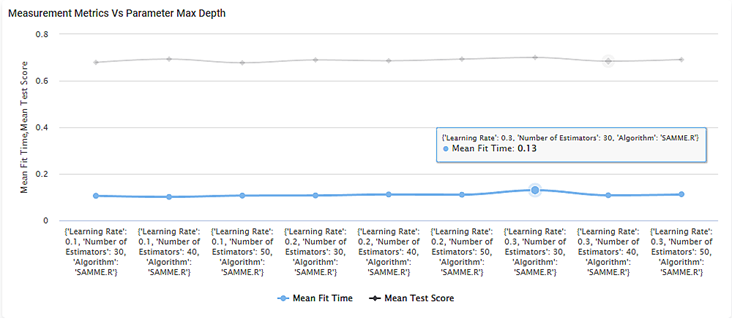
• The two curves are plotted considering all possible combinations of the Number of Estimators, Learning Rates, and Algorithms.
• When you hover over any point on the graphs, you can see the mean fit time or mean test score for a given combination of the above three values.
• For example, the mean fit time is 0.13 for a learning rate of 0.3, the number of estimators equal to 30, and the SAMME.R algorithm.

Hyperparameter Optimization in Support Vector Machine

Hyper Parameter Optimization is used for better Optimization of a given dataset. This feature provides you with a list of parameters that give the best solution for your dataset, among the parameters provided for optimizing the solution. You can select more than one parameter from the list.

The available properties for Hyperparameter Optimization in Support Vector Machine are as shown in the figure below.

While selecting various parameters, note that,

• You can select anyone, multiple, but NOT ALL variables as default parameters from the Default Parameter drop-down. If you select all the variables, then you get a validation error for the selection.
• You can choose not to select any variable as the default parameter.
• After you select the default parameter(s), the remaining parameters appear for selection in the Parameter To Tune drop-down.
• You can select all variables in the Parameters To Tune options. In this case, there are NO variables selected as Default Parameters.
• If a variable is selected as default parameter, the same cannot be selected for tuning. If you select it for tuning, the parameter is removed from the default parameter selection.
• You can select any number of values for all the variables. The values should be entered in the appropriate boxes with a comma separating two values.
• The fields for entering the values for these parameters are displayed accordingly below the two dropdowns.

We select the following values for parameters and properties.

The figure below shows the results of Hyperparameter Optimization in Support Vector Machine.

Inferences:

• The Result page shows
  • Measurement Metrics
  • Best parameters
  • Graphical representation of the variation of Measurement Metrics against Parameter Maximum Depth.
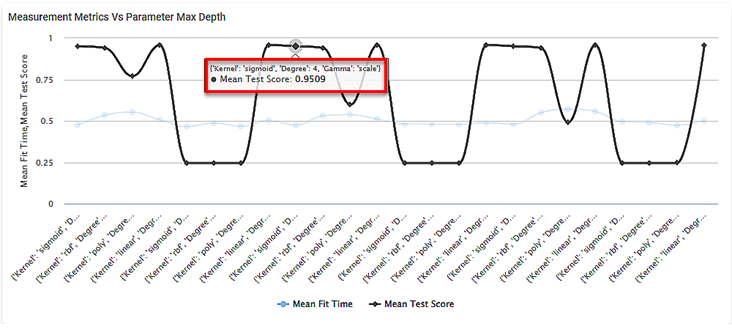
• For example, when Kernel = sigmoid, Gamma = scale, and Degree = 3,
  • Mean Fit Time = 0.4758
  • Mean Test Score = 0.9509
  • Mean Cross Validation Score = 0.9509
• Best parameters:
  • Kernel = linear
  • Gamma = scale
  • Degree = 3
• You can change the selected values and get new Measurement Metrics by clicking the Get Metrics button.
• The graph contains two curves for
  • Mean Fit Time
  • Mean Test Score
• The two curves are plotted considering all possible combinations of the Kernel, Gamma, and Degree values.
• When you hover over any point on the graphs, you can see the mean fit time or mean test score for a given combination of the above three values.
• For example, the mean test score is 0.9509 for the sigmoid kernel, Gamma equal to scale and a degree of four (4).