Chi Square Goodness of Fit Test
Description	Chi Square Goodness of Fit Test determines whether a categorical variable is likely to be derived from a specified distribution. This test is the same as Pearson’s Chi Square test.
Why to use	To check whether a sample data derived from a population is a representative of the population.
When to use	For categorical variables	When not to use	For continuous variables
Prerequisites	The data should be categorical. There should be at least five values in each of the observed data categories. The data should be a random sample of the population. There should be a hypothesis describing how the variable is distributed.
Input	One categorical variable	Output	Chart of Contribution to Chi Square value by category Charts of Observed and Expected values Null and Alternative Hypothesis Computation and Result tables for Chi square Interpretation of the result
Statistical Methods used	Frequency p-value alpha Chi Square	Limitations	It can be used only on categorical data.

Chi Square Goodness of Fit Test is located under Model Studio ( ) in Hypothesis Test, in Statistical Analysis, in the left task pane. Use the drag-and-drop method to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis. Refer to Properties of Chi Square Goodness of Fit Test.

The Chi Square Goodness of Fit Test is a hypothesis test. It tests whether the selected categorical variable is likely to be derived from the specified distribution. A dataset consists of data points. You also have a hypothesis or an idea to imagine how these data points are distributed in the dataset. The Chi Square Goodness of Fit Test gives you a way to check whether the data points actually fit our idea or hypothesis. That is, the test checks whether the data points are really distributed the way you have imagined them to be.

Properties of Chi Square Goodness of Fit Test

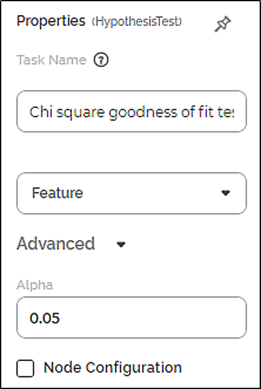
The available properties of the Chi Square Goodness of Fit Test are as shown in the figure given below.

The table below describes the different fields present on the Properties pane of the Chi Square Goodness of Fit Test.

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the name of the task as required.
Feature		It allows you to select the categorical variable for the test.	Only one categorical variable can be selected.
Advanced	Alpha	It allows you to set the level of significance.	The default value is 0.05.
Advanced	Node Configuration	It allows you to select the instance of the AWS server to provide control on the execution of a task in a workbook or workflow.	For more details, refer to Worker Node Configuration.

Example of Chi Square Goodness of Fit Test

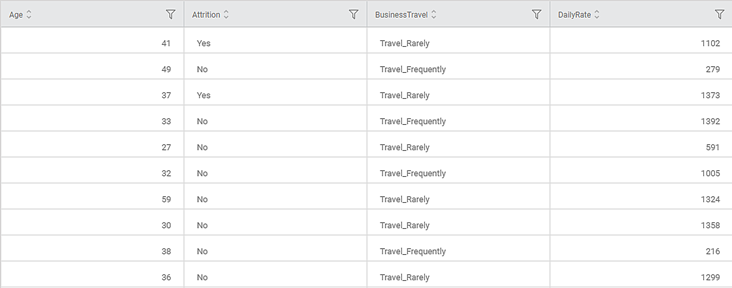
Consider a HR dataset containing features like Age, BusinessTravel, Daily Rate, Department, DistanceFromHome, Education, and so on. A snippet of the input data is shown in the figure given below.

The BusinessTravel feature is selected as the categorical variable for studying the Chi Square Goodness of Fit Test.

The part of the Result page containing charts for the Chi Square Goodness of Fit Test is displayed below.

On this part of the Result Page,

Chart of Contribution to the Chi Square value by Category shows Combined Values depicting the contribution of each BusinessTravel frequency to the calculated Chi Square value.
Chart of Observed and expected Values gives a comparative idea of the contribution of each BusinessTravel frequency to the calculated Chi Square value.

On this part of the Result Page,

Chart of Contribution to the Chi Square value by Category shows Combined Values depicting the contribution of each BusinessTravel frequency to the calculated Chi Square value.
Chart of Observed and expected Values gives a comparative idea of the contribution of each BusinessTravel frequency to the calculated Chi Square value.
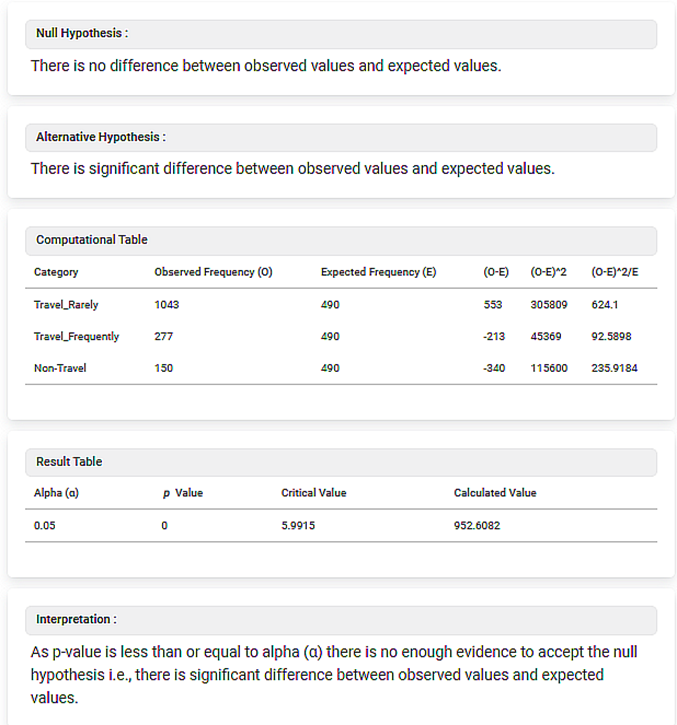
Null Hypothesis assumes that there is no difference between observed and expected values.
Alternative Hypothesis assumes that there is significant difference between observed values and expected values.
Computation table for Chi Square gives the Observed Frequency (O) and Expected Frequency (E) of the BusinessTravel feature in the categories, Travel_Rarely, Travel_Frequently, and Non-Travel. It also shows the values for (O-E), (O-E)², (O-E)²/E.
The Result table for Chi Square gives the Critical Value (952.6082), Calculated Value (5.9915) for Chi Square. It also gives the p value (0) and alpha (0.05).

You observe that the p value is less than alpha. Thus, the Interpretation states that there is not enough evidence available to accept the null hypothesis. Thus, values are not coming from a normal distribution. This is because, there is a significant amount of difference between the observed values and expected values.

Table of Contents