AdaBoost in Classification

AdaBoost in Classification
Description	AdaBoost is a technique in Machine Learning used as an Ensemble Method. AdaBoost is a boosting algorithm that combines the predictions of multiple weak classifiers to create a strong classifier.
Why to use	Improved Accuracy Versatility Feature Selection Handling Complex Data Interpretable Results Robustness to Overfitting
When to use	Weak Learners Imbalance Data Outliers High-Dimensional Data Complex Decision Boundaries	When not to use	Insufficient Data Time and Resource Constraints Class Imbalance Non-Linear Relationships Noisy Data
Prerequisites	If the data contains missing values, use Missing Value Imputation before proceeding with AdaBoost.
Input	Dataset with Weak Classifiers.	Output	Key Performance Index (KPI) Confusion Matrix Graphical Representation
Statistical Methods Used	Weighted Training Data Error Rate Calculation Weighted Voting Stopping Criterion	Limitations	Sensitivity to Noisy Data Susceptible to Overfitting Computationally Expensive Limited to Binary Classification Requires Careful Parameter Tuning

You can find AdaBoost under the Machine Learning section in the Classification category on Feature Studio.
Alternatively, use the search bar to find the AdaBoost algorithm. Use the drag-and-drop method or double-click to use the algorithm in the studio canvas.
Click the algorithm to view and select different properties for analysis.

The basic idea behind AdaBoost is to iteratively train a series of weak classifiers on different subsets of the training data. A weak classifier is a simple model that performs slightly better than random guessing. In each iteration, AdaBoost assigns weights to the training samples. It places more emphasis on the misclassified samples from the previous iteration.

During the training process, AdaBoost adjusts the weights of the training samples so that the subsequent weak classifiers focus on the misclassified ones by the previous weak classifiers. This iterative process continues until a predetermined number of weak classifiers have been trained or a desired level of accuracy.
AdaBoost combines the weak classifiers by assigning weights to each one based on its performance. The weak classifiers' performance determines the consequences, and they make the final classification decision by taking a weighted majority vote.

The advantage of AdaBoost is its ability to handle complex datasets and capture intricate patterns by combining multiple weak classifiers. Additionally, AdaBoost is resistant to overfitting and can generalize well to unseen data.

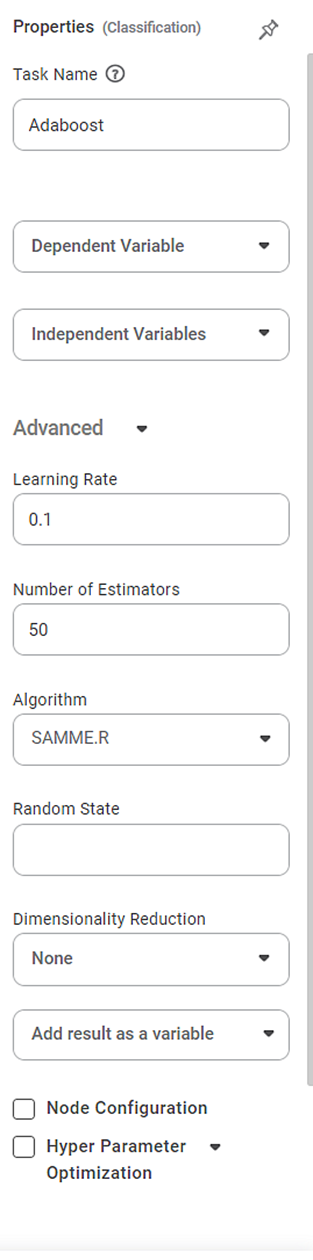
Properties of AdaBoost

The figure below shows the available properties of AdaBoost:-

Field		Description	Remark
Task Name		It is the name of the task selected on the workbook canvas.	You can click the text field to edit or modify the task name as required.
Dependant Variable		It allows you to select the dependent variable	You can choose only one variable. It should be of a Categorical type.
Independent Variable		It allows you to select the independent variable.	You can select more than one variable.
Advanced	Learning Rate	It allows you to change the learning rate accordingly	When the learning rate is higher, it leads to a greater contribution of each classifier.
	Number of Estimators	It allows you to select the number of estimators. Estimator stands for Trees. It takes the input from the user for the number of trees to build the ensemble model.	The default value is 50. It does not have a fixed upper limit. In order to enhance the robustness of AdaBoost, the maximum value is selected.
	Algorithm	It allows you to select between the two given options	The options are SAMME and SAMME.R
	Random State	It allows you to enter the value of the random state.	Enter only numerical value.
	Dimensionality Reduction	It allows you to select the dimensionality reduction method.	You can select only one data field. The available options are None and PCA. The default value is None.

Example of AdaBoost in Classification

In the example provided below, the Superstore dataset is used to apply AdaBoost. The independent variables considered are City, Sales, and Profit, while the dependent variable selected is Category.

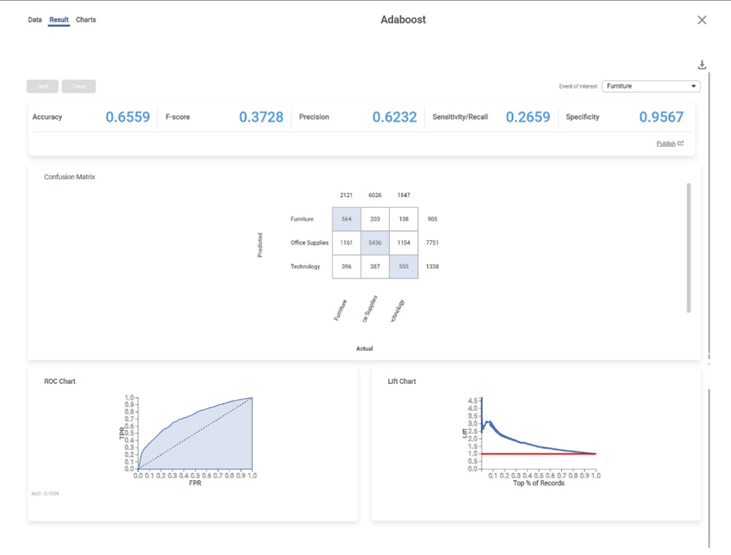
After using the AdaBoost algorithm, the following results are displayed.

The result page displays the following sections.

Section 1 – Key Performance Index (KPI)

The categorical variable's different options are displayed in the top right corner. Here Furniture variable is displayed. The first option appears as the default selected option.

Accuracy – This value represents the accuracy of predictions on the model.
F-Score – This value represents the accuracy of predictions on the selected categorical variable.
Precision – This value represents the number of false positives.
Sensitivity/Recall – This value represents the number of positive instances.
Specificity – This value represents the selected categorical value's ability to predict true negatives.

Field	Description	Remark
Accuracy	Accuracy is the ratio of the total number of correct predictions made by the model to the total number of predictions made. Accuracy = (TP + TN) / (TP + TN + FP + FN) Where, TP, TN, FP, and FN indicate True Positives, True Negatives, False Positives, and False Negatives.	The Accuracy is 0.6559.
F-Score	F-score is a measure of the accuracy of a test. It is the harmonic mean of the precision and recall of the test. F-score = 2 (precision × recall) / (precision + recall) Where, Precision = positive predictive value, which is the proportion of the positive values that are positive. Recall = The ability to correctly identify positive results to get the true positive rate is called sensitivity.	It is also called the F-measure or F₁ score. The F-score is 0.3728.
Precision	Precision is the ratio of the True positive to the sum of the True positive and False Positive. It represents positive predicted values by the model.	Here Precision is 0.6232.
Sensitivity	It measures the test's ability to identify positive results. Sensitivity = TP / (TP + FN) Where, TP = number of true positives FN = number of false negatives	It is also called the True Positive Rate. The value of sensitivity is 0.2659.
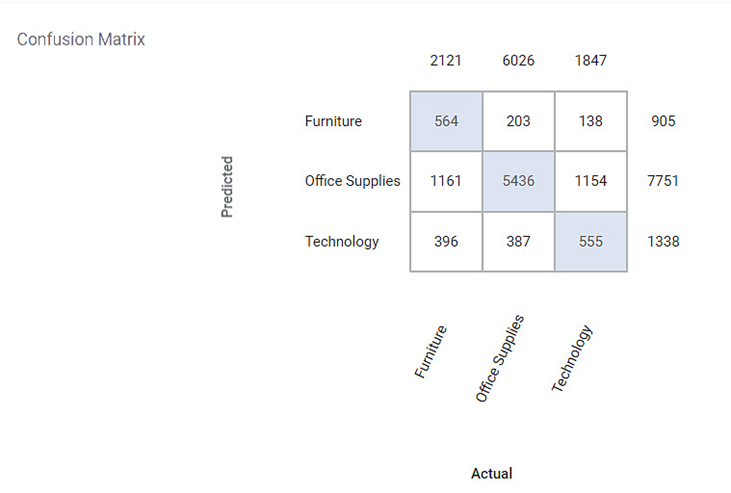
Specificity	It gives the ratio of the correctly classified negative samples to the total number of negative samples: Specificity = TN / (TN + FP) Where TN = number of true negatives FP = number of false positives	It is also called inverse recall. The value of Specificity is 0.9567.

Section 2 – Confusion Matrix

A confusion matrix is a summarized table used to assess the performance of a classification model. The number of correct and incorrect predictions is summarized with count values and broken down by each class.
Following is the confusion matrix for the specified categorical variable. It contains predicted values and actual values for the Category.

The shaded diagonal cells show the correctly predicted categories.
The remaining cell indicates the false prediction categories.

Section 3 – ROC chart

The Receiver Operating Characteristic (ROC) Chart is given below. The ROC curve is a probability curve that measures the performance of a classification model at various threshold settings.

The ROC curve is plotted with a True Positive Rate on the Y-axis and a False Positive Rate on the X-axis.
We can use ROC curves to select the most optimal models based on the class distribution.
The dotted line is the random choice with a probability equal to 50%, an Area Under Curve (AUC) equal to 1, and a slope equal to 1.

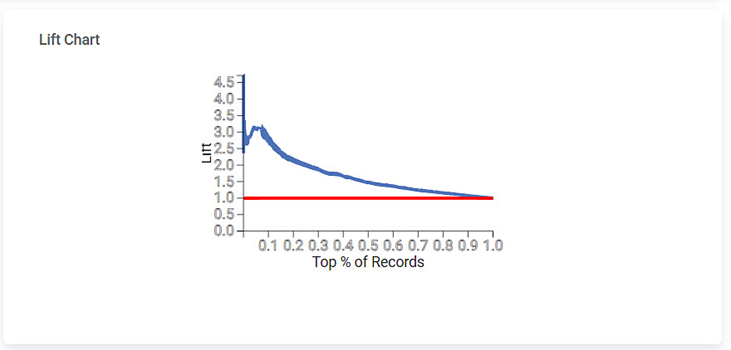
Section 4 – Lift Chart

The Lift Chart obtained is given below. A lift is the measure of the effectiveness of a model. It is the ratio of the percentage gain to the percentage of random expectation at a given decile level. It is the ratio of the result obtained with a predictive model to that obtained without it.

A lift chart contains a lift curve and a baseline.
The curve should go as high as possible towards the top-left corner of the graph.
Greater the area between the lift curve and the baseline, the better the model.
In the above graph, the lift curve remains above the baseline up to 50% of the records and then becomes parallel to the baseline.

Your Rating:

Table of content