LSTM (Long Short-Term Memory)
Description	Forecasting and Prediction of the model include numerical and date dataset.
Why to use	Forecasting Time series
When to use	To classify, process, and make predictions based on time series data.	When not to use	On textual data and categorical data.
Prerequisites	The independent variable should be of interval type. The dependent variable should be of numerical type.
Input	Any dataset that contains time interval as well as numerical type of data.	Output	The predicted value of the dependent variable.
Statistical Methods used	Mean Squared Error Mean Absolute Error	Limitations	LSTMs cannot solve the problem of vanishing gradients. LSTMs take a lot of time to get trained for complex data. LSTMs are prone to overfitting.

LSTM is a model that can be used for solving Univariate and Multivariate time series forecasting problems. LSTM is used to learn from the series of past observations to predict the next value in the sequence. It has the ability to learn the context required to make predictions, rather than having this context pre-specified and fixed.

With LSTM, the user can select multidimensional functionality for the target variable specifically. The multidimensional functionality allows the user to predict the accuracy or predict the model’s accuracy for multiple dimensions. LSTM is a technique that employs data models and uses statistical tools to predict outcomes. Although LSTM cannot perform future analysis with 100% accuracy, it can predict the possible outcome.

LSTM is located under Forecasting in Modeling, in the task pane on the left. Use drag-and-drop method to use algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Refer to Properties of LSTM.

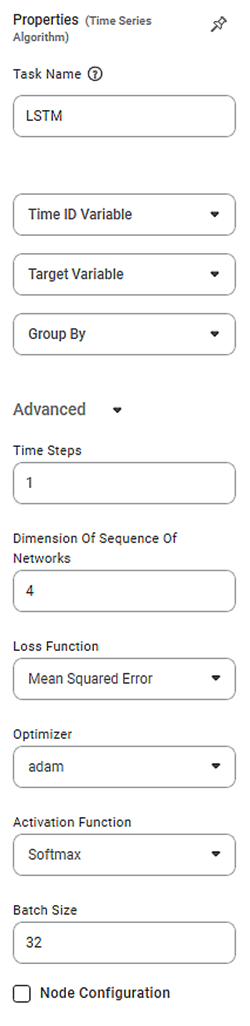
Properties of LSTM

The available properties of LSTM are as shown in the figure given below.

The table given below describes the different fields present on the properties of LSTM.

Field		Description	Remark
Task Name		It displays the name of the selected task.	You can click the text field to edit or modify the name of the task as required.
Time Id Variable		It allows you to select the variable from the drop-down list for which we need to predict the values of the dependent variable.	Only one data field can be selected Data fields with only date values are available.
Target Variables		It allows you to select the experimental or predictor variable(s).	Only one data fields can be selected. Data fields with only numerical values are available.
Group by		It allows you group the values by a column	Only one data field can be selected Only categorical data fields are available
Advanced	Time Steps	It provides feedback from the predicted value going back and forth.	It should be selected as per the data. If the target variables are more than one, time steps can be selected more.
	Dimensions Of Sequence Of Networks	Number of neurons to be used in the model to learn complex pattern from the data.	—
	Loss Function	It is the error between the actual value of the target variable and the predicted value of the target variable. It is the function to be used to calculate the accuracy.	There are two types of loss functions: Mean Absolute Error is a measure of errors between paired and observation expressing the same phenomenon. Mean Squared Error is the difference between the estimated values and the actual value.
	Optimizer	It calculates the learning rate for each parameter present in the model and compares it with other adaptive learning algorithms. It is the function used to increase the performance of the model. Optimizers shape and mold the model into its most accurate possible form with the help of weights.	Adam optimizer is an optimization algorithm that can be used instead of the Classification stochastic gradient descent procedure to update network weights iterative based on training data.
	Activation Function	It is a mathematical equation that determines the output of a neural network. It is used in a network to learn complex patterns in the data. It is used for LSTM blocks.	The two values are – Sigmoid – It is used for binary classification. Softmax – It is used for multi-classification. As it is a neuron based model, it decides whether to fire the next neuron or not.
	Batch Size	It is the function that limits the number of samples to be shown to the network before the weight update can be performed. It is used when fitting the model to control the number of predictions must be made at a time. It sets the limits of the processed records in each batch.	It should be the power of two. Its value depends on the sample of data, usually it is 32. 64,128 are also used while experimenting.

Interpretation of LSTM

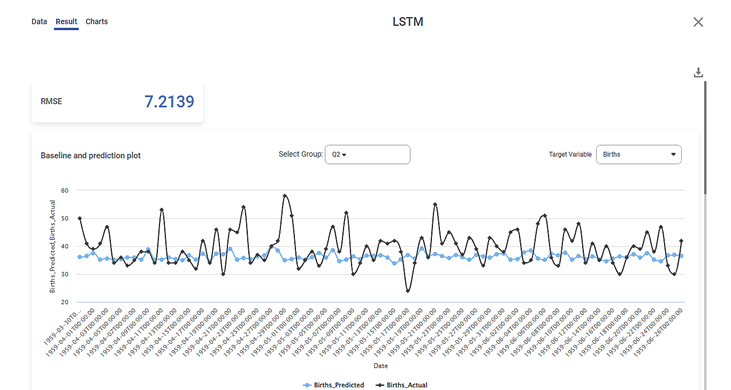
The RMSE value shows the mean of the actual value and the predicted value. The RMSE value should be as small as possible. If the RMSE value is zero, it means it is the best fit model. The best fit model shows there is no difference between the actual value and the predicted value. If the RMSE value is more than zero, you can tweak some parameters to improve the RMSE value.

The chart shows the actual and predicted values for a given time series dataset with a RMSE value. The main aim of plotting this chart is to solve the forecasting problem in univariate and multivariate time series.

In the above example, the RMSE value for Target Variable Birth is 7.2139. We can change some parameters to bring the RMSE value close to zero.

Table of Contents